中3数学「4月春休み明け実力テスト対策問題」です。中1~中2で履修した内容で、小問集合、方程式文章題、関数、図形問題で構成しています。
(新中3数学)4月春休み明け実力テスト対策問題
問1 次の問いに答えなさい。(小問集合)

(5)𝑥が2増加するとき𝑦は6減少し、点(−2,8)を通る一次関数の式を求めなさい。
(6)−2𝑥+9𝑦=4𝑥−𝑦=17 の方程式を解きなさい。
(7)正十角形の内角の和を求めなさい。
(8)母線が6cm、半径が4cmの円すいの側面積を求めなさい。
(9)ある中学校の生徒8人の通学時間を調べると次のようであった。この8人の通学時間の中央値を求めよ。
調査結果【 6分 9分 3分 4分 5分 15分 7分 13分】
(10)あたりが3本、はずれが4本の7本のくじを、同時に2本のくじをひくとき、2本ともはずれをひく確率を求めよ。
問2 (連立方程式文章題)
ある中学校では、3年生230人を対象に体育・美術・音楽の3教科の選択授業を実施しています。前期では、美術を選んだ生徒は体育を選んだ生徒の40%より2人多く、後期では、体育を選んだ生徒が4人減り、音楽を選んだ生徒が2人減ったため、体育を選んだ生徒は音楽を選んだ生徒のちょうど2倍になりました。前期に体育を選んだ生徒の数をx人、音楽を選んだ生徒の数をy人として、次の問いに答えなさい。ただし、3年生全員が3教科のうち1教科を必ず選択するものとします。
(1) 前期の美術を選んだ生徒の数をxだけを用いて表しなさい。
(2) x, y についての連立方程式を作りなさい。
(3) (2)の連立方程式を解き、後期に美術を選んだ生徒の数を求めなさい。
問3 (関数総合)
下の図のように、直線y=x+4と直線y=ax+10がある。この2直線とx軸との交点をそれぞれA、B(2,0)とするとき、次の問いに答えよ。
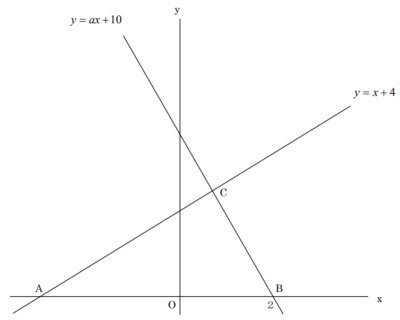
(1)直線y=ax+10の傾きを求めよ。
(2)直線y=x+4と直線y=ax+10の交点Cの座標を求めよ。
(3)点Bを通り、直線ACと平行な直線の式を求めよ。
(4)点Aを通り、△ABCの面積を2等分する直線の式を求めよ。
(5)点Cを通り、△ABCの面積を3等分する直線の中で、切片が正の数となる直線の式を求めよ。
問4 (図形総合)
下の図のように、1辺が4cmの正方形ABCDがある。辺BC上に、2点B、Cと異なる点Eをとり、点Dと点Eを結ぶ。点Aから線分DEに垂線をひき、その交点をFとする。また、点Cから線分DEに垂線をひき、その交点をGとする。CE=3cm、DE=5cmのとき、次の問いに答えなさい。
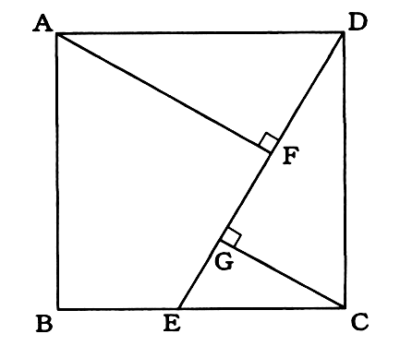
(1)△AFD≡△DGCであることを証明せよ。
(2)DFの長さを求めよ。
(新中3数学)4月春休み明け実力テスト対策問題の解答
問1
(1)48
(2)8𝑎2𝑏3
(3)8𝑎−6𝑏
(4)a=(3𝑏−7)/2
(5)𝑦=−3𝑥+2
(6)(𝑥,𝑦)=(5,3)
(7)1440°
(8)12𝜋𝑐𝑚2
(9)6.5
(10)2/7
問2
(1)0.4x+2
(2)
x+y+0.4x+2=230
x-4=2(y-2)
(3)
(2)の連立方程式を解くと、
x=120 y=60
230-(116+58)=56
(答え)56
問3
(1)a=-5
(2)(1,5)
(3)y=x-2
(3)y=5/11x+20/11
(4)y=8/3x+10/3
問4
(1)△AFDと△DGCにおいて
AD=DC(仮定)…①
∠AFD=∠DGC=90°…②
∠ADF=90°-∠GDC…③
∠DCG=90°-∠GDC…④
③④より∠AFD=∠DCG…⑤
①②⑤より直角三角形の斜辺と1つの鋭角がそれぞれ等しい
よって△AFD≡△DGC
(2)12/5cm


コメント