中1数学「平面図形のポイントまとめ及び定期対策テスト問題」です。
平面図形のポイントまとめ(中1数学)
■直線と図形
- 直線…まっすぐに限りなくのびている線のことを直線という。
- 線分…直線の一部分で、両端のあるものを線分という。
- 半直線…1点を端 として一方にだけのびたものを半直線という。
- 距離…2点 A, Bを結ぶ線のうち、もっとも短いものは線分AB の長さで、これを2点 A, B 間の距離という。
ABと書いて、線分ABの長さを表すことがある。
・角…∠ABC と表し、角ABCと読む。
・交点…2つの線が交わる点。
■垂直
- 2直線 AB, CD が垂直に交わるとき、AB⊥CD と表す。また、2直線ABとCDが垂直であるとき、その一方を他方の垂線という。
- 点Aから直線BCに垂線をひき、直線BCとの交点をHとすると、線分AHは、点Aと直線BC上の点を結ぶ線分のうち、もっとも短いものになり、この長さを点Aと直線BCとの距離という。
■平行
- 2直線 AB, CD が平行のとき, AB//CDと表す。
- 2直線 0, m が平行であるとき、点Pをl上のどこにとっても, 点 Pと直線mとの距離は一定で、この距離を平行な2直線l, m 間の距離という。
■多角形
いくつかの線分で囲まれた図形。三角形ABCは、△ABCと表す。
いくつかの線分で囲まれた図形。三角形ABCは、△ABCと表す。
■平行移動
図形を、一定の方向に、一定の距離だけ動かす移動を、平行移動といいます。
図形を、一定の方向に、一定の距離だけ動かす移動を、平行移動といいます。
- 対応する2点を結ぶ線分は、長さが等しく平行である。
- 対応する図形の線分は、長さが等しく平行である。
■回転移動
図形を、1つの点を中心として、一定の角度だけ回転させる移動を、回転移動といいます。このとき、中心とする点を、回転の中心といいます。特に、 図形を180°回転させる回転移動を、点対称移動というので覚えておきましょう。
図形を、1つの点を中心として、一定の角度だけ回転させる移動を、回転移動といいます。このとき、中心とする点を、回転の中心といいます。特に、 図形を180°回転させる回転移動を、点対称移動というので覚えておきましょう。
- 対応する2点は、回転の中心からの距離が等しい。
- 図形のどの点も、回転の中心の回りに等しい角度だけ回転する。
■対称移動
図形を、ある直線を折り目として折り返した位置に移す移動を、対称移動といいます。このとき、折り目とした直線を、対称の軸といいます。
図形を、ある直線を折り目として折り返した位置に移す移動を、対称移動といいます。このとき、折り目とした直線を、対称の軸といいます。
- 対応する2点を結ぶ線分は、対称の軸によって垂直に2等分される。
■直線図形
- 線分…まっすぐに限りなくのびている直線といい、その一部のでその両端のあるものです。
2点間の距離…2点A,Bをつなぐ線のうち。もっとも短い線分ABのの長さ。 - 垂直…2直線AB、CDが交わってできる角が直角であるとき。ABとCDは垂直であるといい、AB⊥CDと表します。
- 平行…2直線AB、CDが交わらないとき、ABとCDは平行であるといい、AB//CDと表します。
【対策問題】平面図形
【問1】次の図について、次の問いに答えなさい。
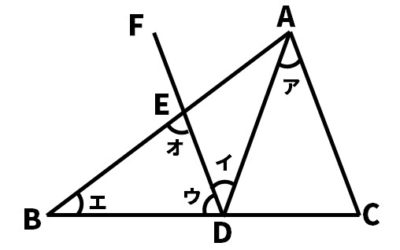
(1)イの角を、A~Fの記号で使って表しなさい。
(2)ア~オの角のうち、∠BDEはどれですか。記号で答えなさい。
(3)点Eのように2つの線が交わる点を何といいますか。
【問2】次の図は、△ABCを直線mにそって5cm平行移動して△PQRをつくったものです。次の問いに答えなさい。
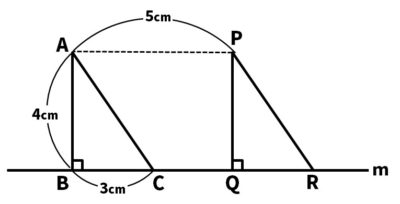
(1)線分CQの長さを求めなさい。
(2)四角形ACRPの面積を求めなさい。
(3)△ABCが動いたあとにできる部分の面積を求めなさい。
直線と図形の定期テスト過去問分析問題の解答
【問1】
(1)∠ADE(∠EDA,∠ADF,∠FDA)
(2)ウ
(3)交点
【問2】
(1)2cm
(2)20cm2
(3)26cm2


コメント