中1数学「データの活用・資料の整理のポイントまとめ及び対策問題」

中1数学「データの活用・資料の整理のポイントまとめ及び対策問題」です。最近では、度数分布表の問題にならび、よく出題されるようになっているので慣れておきましょう。

データの活用・資料の整理のポイント
【対策問題】データの活用・資料の整理
1. 【解答】データの活用・資料の整理

データの活用・資料の整理のポイント

■ヒストグラムのポイント
ヒストグラムは、階級の幅を底辺、度数の高さを長方形を順に並べて示したグラフです。柱状グラフともいいます。またヒストグラムで、各長方形の上の辺の中点を順に結んだものを、度数折れ線（度数分布多角形）といます。ただし、両端の1つ外側の階級の度数を0とします。

階級…資料を区間に分けて整理するとき、分けた区間。
階級の幅…区間の幅
階級値…階級の中央の値
度数…各階級に入っている資料の個数
度数分布表…階級ごとに度数をまとめた表。

■ヒストグラムの書き方
ヒストグラムは、階級の幅を横の辺、度数の縦の辺とする長方形を順に書いていきます。度数折れ線は、各長方形の上の辺の中点を順に結んでいきます。そして、両端の階級の1つ外側の階級の度数を0として、横軸と折れ線が閉じるようにして書いて終了です。

■度数分布表のポイント
度数分布表は、階級に応じで度数を整理した表のことです。

階級…資料を整理したときの1つ1つの区間
階級値…階級の真ん中の値
度数…各階級に入る資料の個数をその階級の度数といいます。
相対度数＝各階級の度数/度数の合計　ふつう、小数第2位まで求めます。（＝小数第3位を四捨五入）
割合（％）＝相対度数×100

【対策問題】データの活用・資料の整理

【問1】次の図は、あるクラスの女子のソフトボ－ル投げの記録をヒストグラムに表したものである。

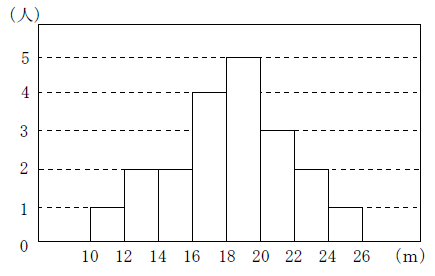
このとき、次の問いに答えなさい。

このクラスの女子の人数を求めよ。
階級の幅は、何ｍですか。
度数が4である階級の階級値を求めよ。
このクラスの女子の記録の中央値が入っている階級の階級値で答えよ。
この表の最頻値を階級値で答えよ。
10ｍ以上12ｍ未満の生徒の相対度数を求めよ。
18ｍ以上20ｍ未満の生徒の相対度数を求めよ。
記録が18ｍ未満の生徒の人数は、全体の何％にあたるか求めよ。
18ｍ以上20ｍ未満の生徒の割合は、全体の何％にあたるか求めよ。
この20人の記録の平均値を求めなさい。

【問2】次の表は、ある中学校の男子の体重を測定してつくった度数分布表で、度数が1か所欠けている。

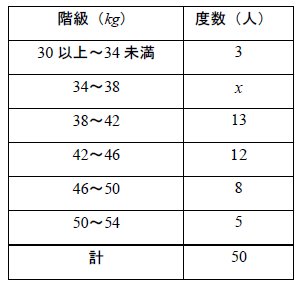
次の問いに答えなさい。

（1）階級の真ん中の値を何というか答えよ。
（2）xにあてはまる度数を答えよ。
（3）階級値32kgで表される階級値の相対度数を求めよ。
（4）階級値44kgで表される階級値の相対度数を求めよ。
（5）階級値52kgで表される階級値の相対度数を求めよ。
（6）体重38kg～42kg未満の人は、全体の何％か求めよ。
（7）体重46kg～50kg未満の人は、全体の何％か求めよ。
（8）体重が重い人から数えて、12番目の人の階級はどこに入るか階級値で答えよ。
（9）体重が重い人から数えて、6番目の人の階級はどこに入るか階級値で答えよ。
（10）最頻値を度数分布表から求めよ。