中学数学「相似な図形の練習問題」です。定期テスト対策として、典型問題を解いて備えよう。
相似な図形の対策問題の一覧
・三角形の相似条件と証明
・平行線と線分の比
・線分の比と相似比
・中点連結定理
・相似な図形の面積
・相似な立体の表面積・体積
などから構成しています。
【対策問題】三角形の相似条件と証明
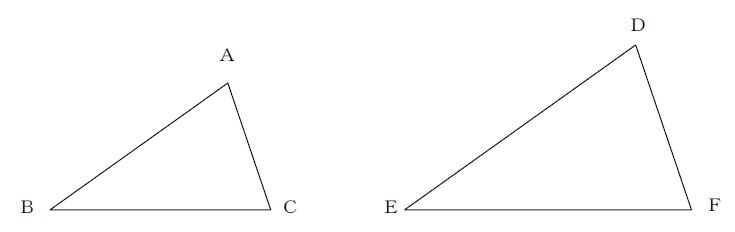
図で、∠A=∠D、∠C=∠Fが等しいとき、△ABCと△DEFが相似であることを証明せよ。
【解答】
△ABCと△DEFにおいて
∠BAC=∠EDF(仮定)…①
∠BCA=∠EFD(仮定)…②
①②より、2組の角がそれぞれ等しい。
よって、△ABC∽△DEFとなります。
■三角形の相似条件
- 3組の辺の比がすべて等しい。
- 2組の辺の比とその間の角がそれぞれ等しい。
- 2組の角がそれぞれ等しい。
■理由になりうるもの
- 仮定より
- 共通だから
- 対頂角だから
- ℓ//mで錯角が等しいから
- ℓ//mで同位角が等しいから
- 弧ABの円周角だから
- 中点連結定理より
などがあります。しっかり、問題を文を読んで、上記の(理由)になりえないか探しましょう。また、相似の証明では、「2組の角がそれぞれ等しい。」の条件にならないかを探り、証明していくのが王道です。それが該当しないとき、辺の長さや辺の比から、他の条件を探っていきます。
【対策問題】平行線と線分の比
次の図を見て、問いに答えなさい。
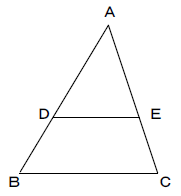
(1)AD=8、AB=12、DE=6、DE//BCのとき、BCの値を求めよ。
(2)AD=6、AB=9、AC=12、DE//BCのとき、AEの値を求めよ。
(3)AB=18、DE=3、BC=9、DE//BCのとき、BDの値を求めよ。
(4)AD=10、DE=3、BC=9、DE//BCのとき、BDの値を求めよ。
次の図を見て、問いに答えなさい。
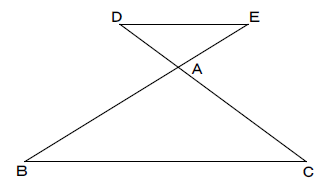
(5)DE=6、BC=9、DA=4、DE//BCのとき、ACの値を求めよ。
(6)AE=9、AB=15、DA=6、DE//BCのとき、ACの値を求めよ。
(7)次の図で、DE=9、BC=15、AE=6、DE//BCのとき、ABの値を求めよ。
次の図を見て、問いに答えなさい。

(8)AD=4、DB=8、AE=5、DE//BCのとき、CEの値を求めよ。
(9)AD=3、DB=7、AC=20、DE//BCのとき、CEの値を求めよ。
(10)BC=8 、D、Eがそれぞれ辺AB、辺ACの中点であるとき、DEの値を求めよ。
【解答】
■相似の三角形の線分比の求め方
- 相似の組を見つけ出す。「帽子型」と「砂時計型」が中心。
- 対応する辺に気をつけて、比例式を完成。
- それを解く。普通、簡単な整数比で表すので、小数や分数の場合は、両方の倍数をかけるなどして整理する。
- 9
- 8
- 12
- 20
- 6
- 9
- 9
- 10
- 14
- 4
【対策問題】線分の比と相似比
【問1】

図は、△ABC∽△DEFでAB=4、DE=8です。
(1)相似比を求めなさい。
(2)辺ACの長さを求めなさい。
【問2】

図において、△ABC∽△DEFのとき、AB=6、AC=5、DE=12のとき、辺DFの長さを求めなさい。
【解答】
【問1】
(1)相似比を表すと
AB:DE=4:8
=1:2
(2)辺ACの長さを求めると
AC=xとして、
2:1=6:x
2x=6
x=3
したがって、AC=3となります。
【問2】
相似比は6:12=1:2だから、DF=xとすると
1:2=5:x
x=10
よって、DF=10となります。
1つの図形を、形を変えずに拡大または縮小して得られる図形は、もとの図形と相似であるといい、記号∽を使って表します。
 図では、△ABCと、その各辺を2倍に拡大した△DEFがあります。
図では、△ABCと、その各辺を2倍に拡大した△DEFがあります。
2つの三角形が相似であることを記号∽を使って表すと
△ABC∽△DEFとなります。(対応させる必要があります。)
辺ABと辺DEの長さの関係は、
DE=2AB(もし、3倍に拡大されたものであるのなら、DE=3AB)
∠Aと∠Dの大きさの関係は
∠A=∠D
【対策問題】中点連結定理
【問1】次の図の△ABCで、点D,E,Fは、それぞれ辺AB、BC、CAの中点です。辺DEFの周の長さを求めなさい。
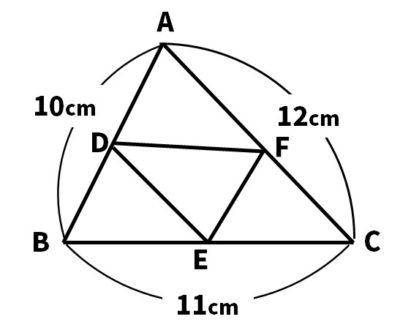
【問2】次の図の△ABCで、辺BCの中点をD、辺CAを3等分する点E,Fとし、ADとBFの交点をGとするとき、次の問いに答えなさい。
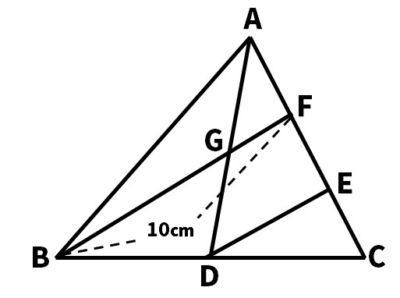
(1)DEの長さを求めなさい。
(2)BGの長さを求めなさい。
【解答】
【問1】
DF=1/2BC=5.5cm
DE=1/2AC=6cm
EF=1/2BA=5cm
よって、辺DEFの周の長さは
5.5+6+5+=16.5cm
(答え)16.5cm
【問2】
(1)△CBFで中点連結定理を使う。
(答え)5cm
(2)△ADEで中点連結定理を使い、BF-GFでBGの長さを求める。
(答え)7.5cm
【対策問題】相似な図形の面積
【問1】次の図について、次の問いに答えなさい。
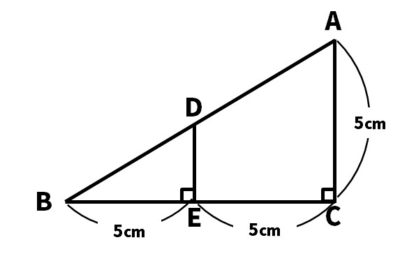
(1)△ABCと△DBEの相似比を求めなさい。
(2)△ABCと△DBEの周の長さの比を求めなさい。
(3)△ABCと△DBEの面積比を求めなさい。
【問2】次の図で、四角形ABCDと四角形EBGFはいずれも正方形で、PとQの面積比は、4:5です。これについて、次の問いに答えなさい。
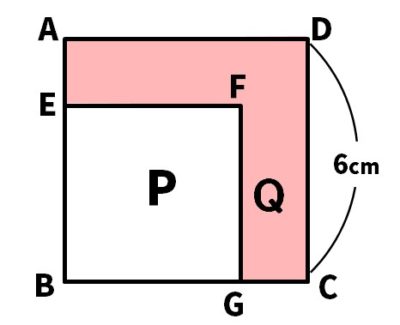
(1)Qの面積を求めなさい。
(2)GCの長さを求めなさい。
【解答】
・周の長さの比はa:b
・面積の比はa2:b2
【問1】
(1)2:1
(2)2:1
(3)4:1
【問2】
(1)20cm2
(2)2cm
【対策問題】相似な立体の表面積・体積
【問1】図のように、相似な2つに四角柱P,Qがあって、PとQの相似比は4:3である。このとき次の問いに答えなさい。
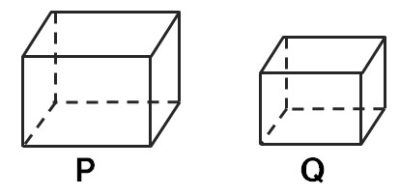
(1)Qの表面積が135cm2のとき、Pの表面積を求めなさい。
(2)Pの体積が192cm3のとき、Qの体積を求めなさい。
【問2】図のような円錐を、母線OAを3等分する点B,Cを通り、底面に平行な平面で切って、3つの立体P,Q,Rに分けるとき、次の問いに答えなさい。
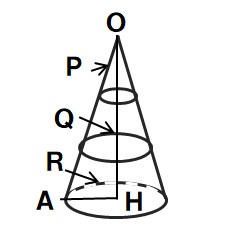
(1)立体Pと立体Qの側面積の比を求めなさい。
(2)OH=18cm,AH=6cmとするとき、立体Rの体積を求めなさい。
【解答】
・表面積の比はa2:b2
・体積の比はa3:b3
【問1】
(1)16:9=x:135
9x=2160
x=240
(答え)240cm2
(2)64:27=192:x
64x=5184
x=81
(答え)81cm3
【問2】
(1)1:4
(2)
立体の体積
=1/3×36×18
=216
求める体積R
=216×19/27
=152
(答え)152cm3


コメント