中2数学「3学期学年末テスト予想問題」です。中学2年生の学年末テストでは、「図形の証明」が大きなテーマとなります。図形の証明は、見た目だけでなく、論理的に正しい手順で理由を述べる力が求められます。この問題では、図形の性質を深く理解し、それを論理的に証明する方法をしっかり身につけておくことが重要です。
この記事では、図形の証明における基本的な考え方や証明方法、よく出題される問題パターンを解説します。しっかりとした対策をして、学年末テストを自信を持って乗り切りましょう！
| テストが異なる場合は、該当するテストを解きましょう！ | |||
|---|---|---|---|
| テスト | 中1数学 | 中2数学 | 中3数学 |
| 1学期中間 | 小学校復習・正負の数 | 文字式 | 展開①・因数分解① |
| 1学期期末 | 四則の計算 | 連立方程式① | 確率・展開②・因数分解② |
| 2学期中間 | 一次方程式① | 連立②・一次関数① | 二次方程式②・二次関数① |
| 2学期期末 | 一次方程式②・比例・反比例 | 一次関数利用・角度 | 二次関数②・相似① |
| 3学期学年末 | 平面図形・空間図形 | 今回：図形の証明 | 総復習・相似②・三平方の定理 |
中学2年生数学学年末予想テスト問題
問1 次の（ ）にあてはまる語句や式を答え闇斎。
（1）「〇〇ならば、□□である。」ということがらについて、〇〇の部分を（ ア ）といい、□□の部分を（ イ ）という。
（2）AB＝ACである二等辺三角形で、∠Aを頂角、∠Bと∠Cを（ ）という。
（3）合同な図形では、（ ）する線分の長さや角の大きさは等しい。
（4）「△ABCでAB＝BCならば、∠A＝∠Cである。」の逆は、「△ABCで、（ ）。」となる。
（5）直角三角形で直角に対する辺を（ ）という。
（6）平行四辺形の定義は、「（ ）である四角形」である。
（7）次の文は、いろいろな四角形の述べたものである。
・4つの角がすべて等しい四角形を（ ア ）
・4つの辺がすべて等しい四角形を（ イ ）
・4つの辺、4つの角がすべて等しい四角形を（ ウ ）という。
（8）ひし形の対角線は（ ）に交わる。
（9）1つの内角の大きさが、1つの外角の大きさの8倍である正多角形は、（ ）である。
（10）2点（-3,-8）（3,2）を通る直線の式は（ ）である。
問2 下の図で、AB＝AD、∠ABC＝∠ADEである。次の問いに答えなさい。
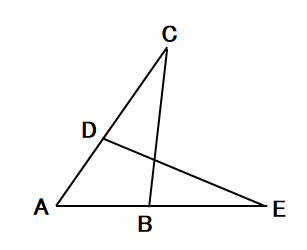
（1）△ABCと合同な三角形をいいなさい。
（2）（1）で使った合同条件をいいなさい。
問3 次の図で∠ｘの大きさを求めなさい。
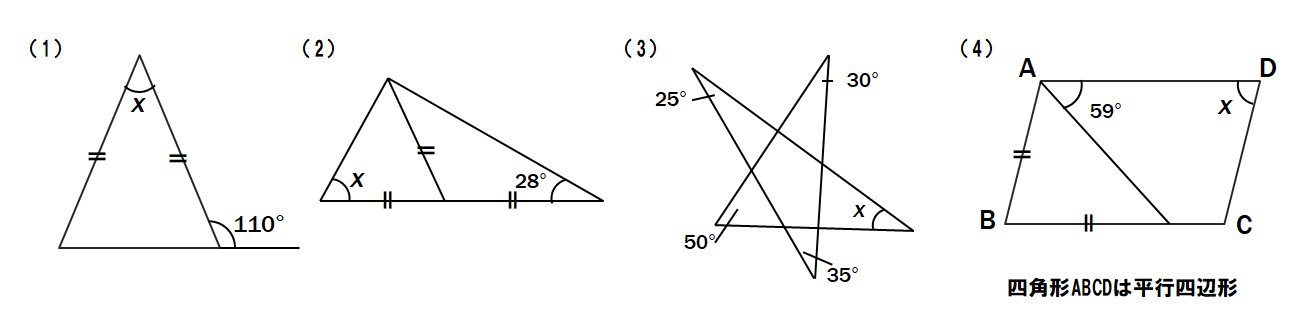
問4 次の図で、点Eは∠ABCの二等分線と∠ACDの二等分線との交点である。∠E＝25°のとき、∠Aの大きさを求めなさい。
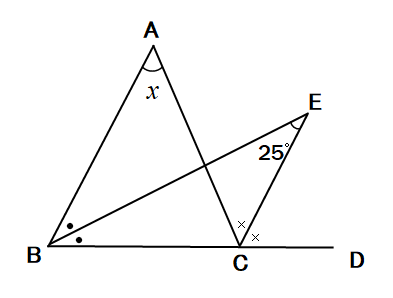
問5 次の図で、AP＝BQ、AQ＝BPならば、∠A=∠Bであることを証明しなさい。
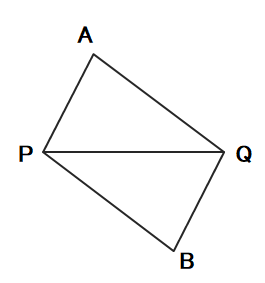
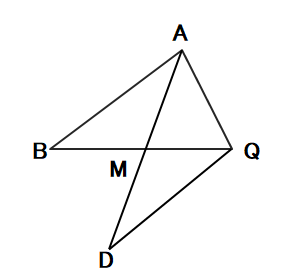
問6 次の図のように、△ABQの辺BQの中点をMとして、AMの延長上にAM＝MDとなる点Dをとる。このとき、AB＝DQであることを証明しなさい。
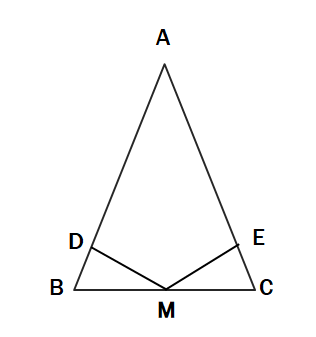
問7 二等辺三角形ABCの底辺BCの中点Mから、それぞれ辺AB、ACに垂線MD、MEをひく。このとき、△BDM≡△CEMであることを証明せよ。
中学2年生数学学年末予想テスト解答
問1
（1）ア仮定 イ結論
（2）底角
（3）対応
（4）∠A＝∠Cならば、AB＝BCである
（5）斜辺
（6）2組の向かい合う辺がそれぞれ平行
（7）ア長方形 イひし形 ウ正方形
（8）垂直
（9）正十八角形
（10）ｙ＝5/3ｘ-3
問2
（1）△ADE
（2）1組の辺とその両端の角がそれぞれ等しい。
問3
（1）40° （2）62° （3）40° （4）62°
問4 50°
問5
△APQと△BQPで
仮定より、AP＝BQ…①
AQ＝BP…②
PQは共通な変なので、PQ=QP…③
①②③より3組の辺がそれぞれ等しいので、
△APQ≡△BQP
合同な三角形では、対応する角は等しいので
∠A＝∠B
問6
△ABMと△DQMで
仮定より、AM＝DM…①
仮定より、BM＝QM…②
対頂角より、∠AMB＝∠DMQ…③
①②③より、2組の辺とその間の角がそれぞれ等しいので
△ABM≡△DQM
合同な図形は、対応する辺は等しいので
AB＝DQ
問7
△BDMと△CEMで
仮定より、∠BDM＝∠CEM＝90°…①
仮定より、BM＝CM…②
二等辺三角形の2つの底角は等しいので、
∠DBM＝∠ECM…③
①②③より
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△BDM≡△CEM
コメント