【応用】高校入試数学模擬テスト｜偏差値60以上の高校受験合格のために

【応用】高校入試数学模擬テスト｜偏差値60以上の高校受験合格のためにです。私立高校の受験対策としてもご利用いただけます。

問1　計算集合　（5問×8＝40点）
問2　方程式文章題　（1問×10点）
問3　関数　（3問×6＝18点）
問4　平面図形　（3問×6＝18点）
問5　空間図形　（2問×7＝14点）

の構成となっています。（100点満点）

偏差値の目安
100点-偏差値67.5
90点以上-偏差値65以上
75点以上-偏差値60以上
55点以上-偏差値55以上
40点以上-偏差値50以上

高校入試数学模擬テスト応用問題

問1　小問集合
次の問いに答えなさい。

問2　方程式文章題
Ａ君とＢ君が山登りのトレーニングをした。２人は、同時にスタート地点を出発し、同じコースで1200ｍ先のゴール地点に向かった。Ａ君は、毎分40ｍの速さでスタート地点からｘｍ進んだ地点（以下「ｘｍ地点」という。）まで行き，ｘｍ地点からゴール地点までは毎分30ｍの速さで行った。また、Ｂ君は毎分40ｍの速さでスタート地点（以下「ｙｍ地点」という。）まで行き、そこで５分間休憩した後，毎分60ｍの速さでｙｍ地点からゴール地点まで行った。スタート地点から見て、ｙｍ地点は、ｘｍ地点より120ｍ先である。このとき，次の問いに答えよ。２人は、同時にゴール地点に着いた。ｘ，ｙについての連立方程式を作れ。また，ｘ，ｙの値を求めよ。

問3　関数

問4　平面図形

問5　空間図形

高校入試数学模擬テスト応用問題の解答・解説

問1　小問集合

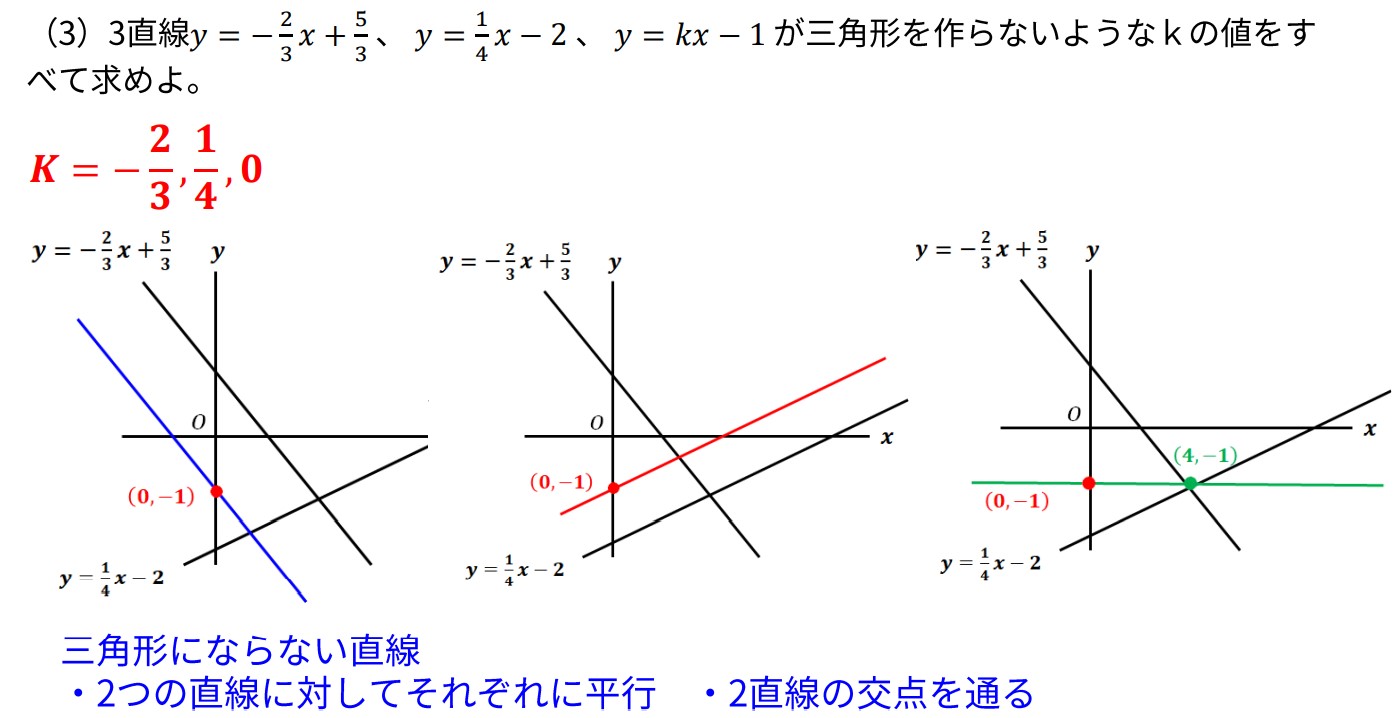
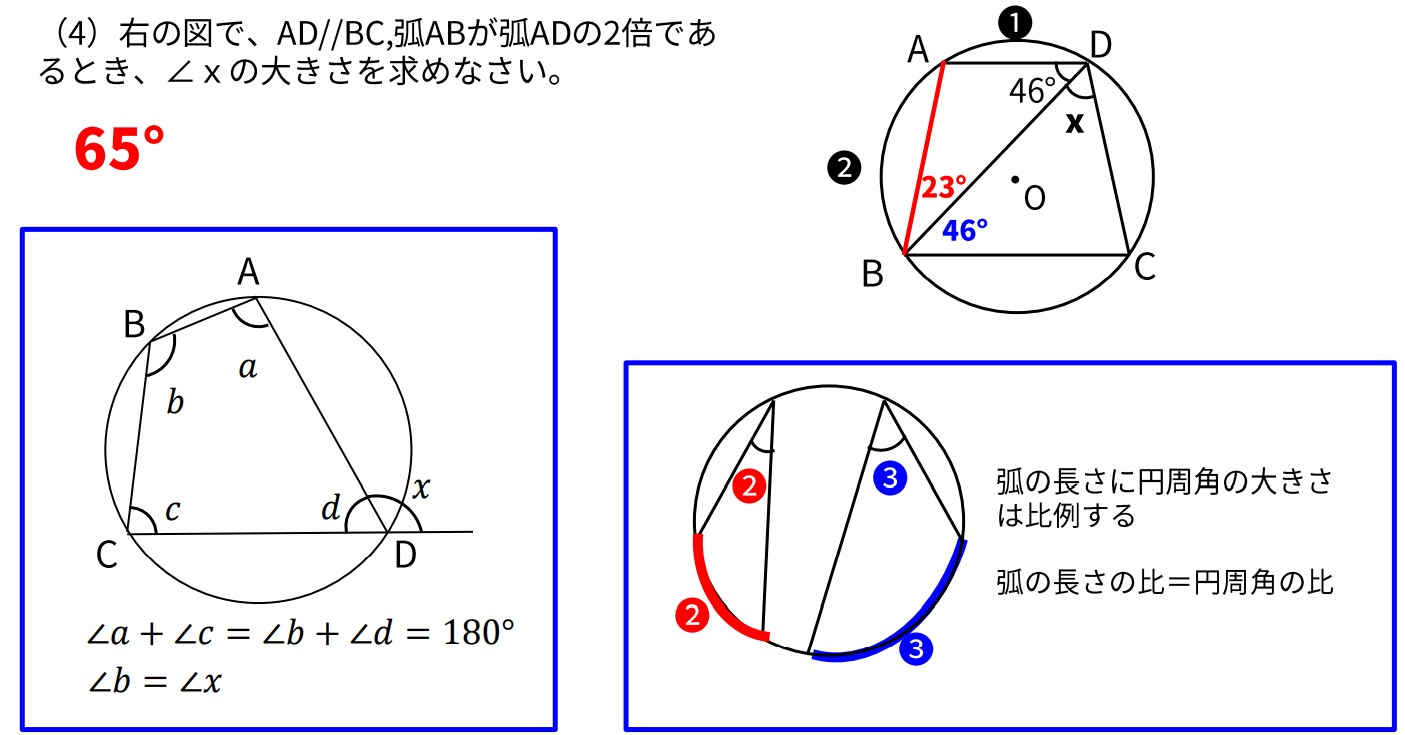
問2　方程式文章題

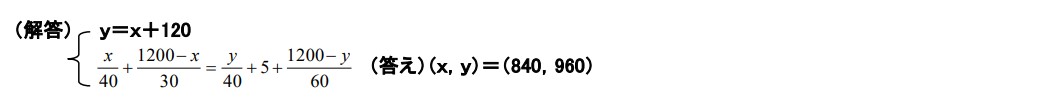
問3　関数

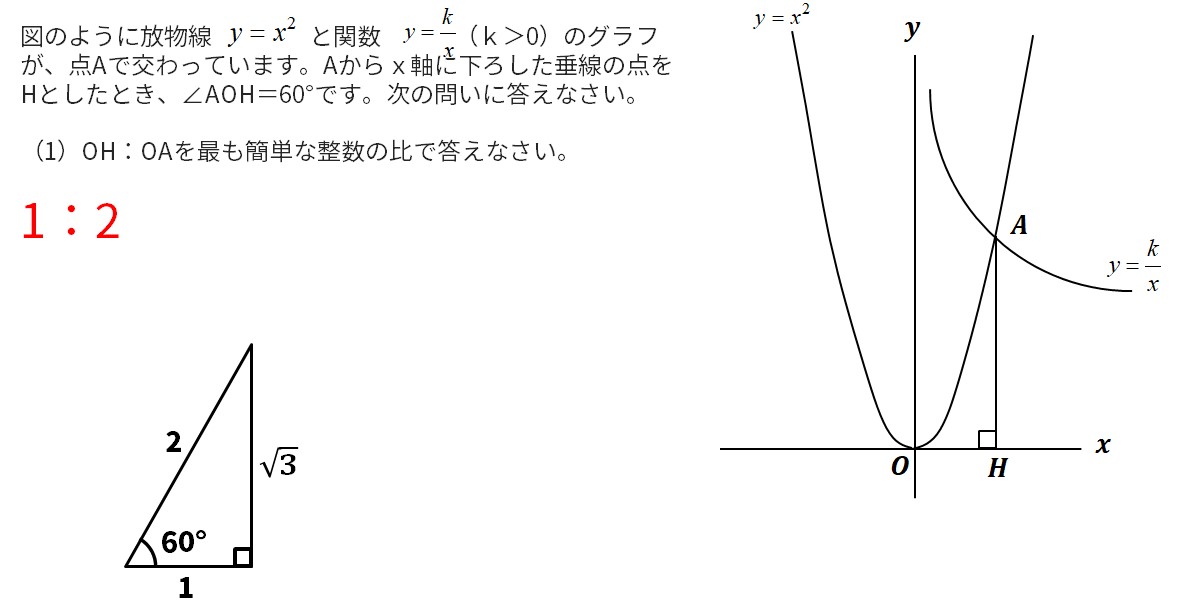
特別な直角三角形1:2:√3を利用する。

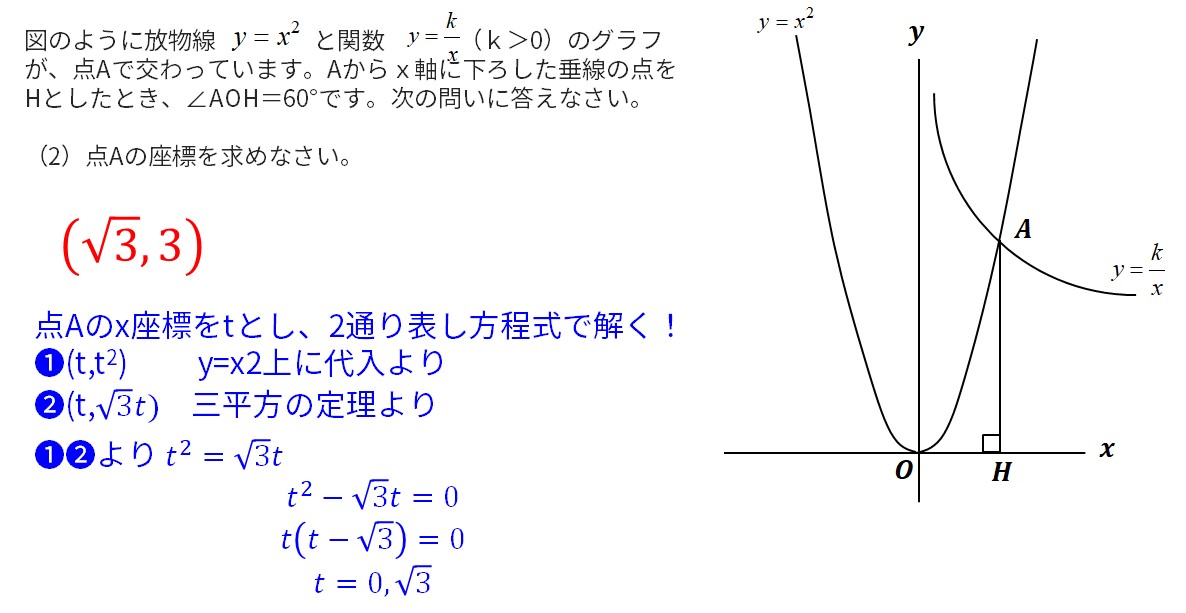
点Aのx座標をtとし、2通り表し方程式で解く！
➊(t,t²) 　　y=x²上に代入より
➋(t,√3𝑡)　三平方の定理より
➊➋より 𝑡²=√3𝑡
𝑡²−√3 𝑡=0
𝑡(𝑡−√3)=0
𝑡=0,√3

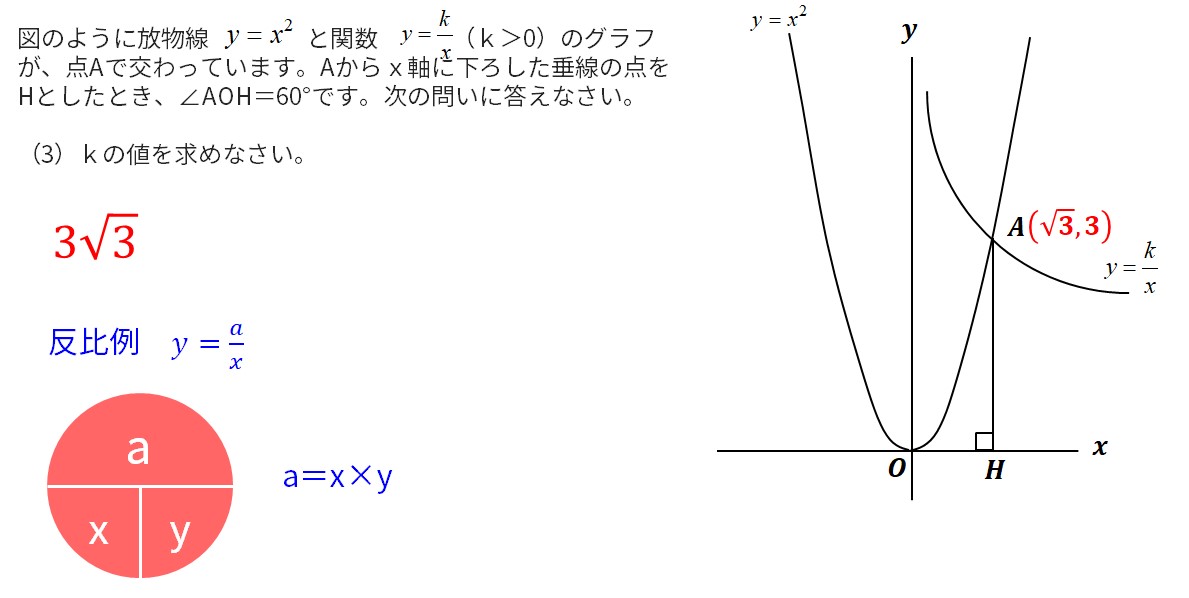
反比例の比例定数は、xの値×ｙの値で求める。

問4　平面図形

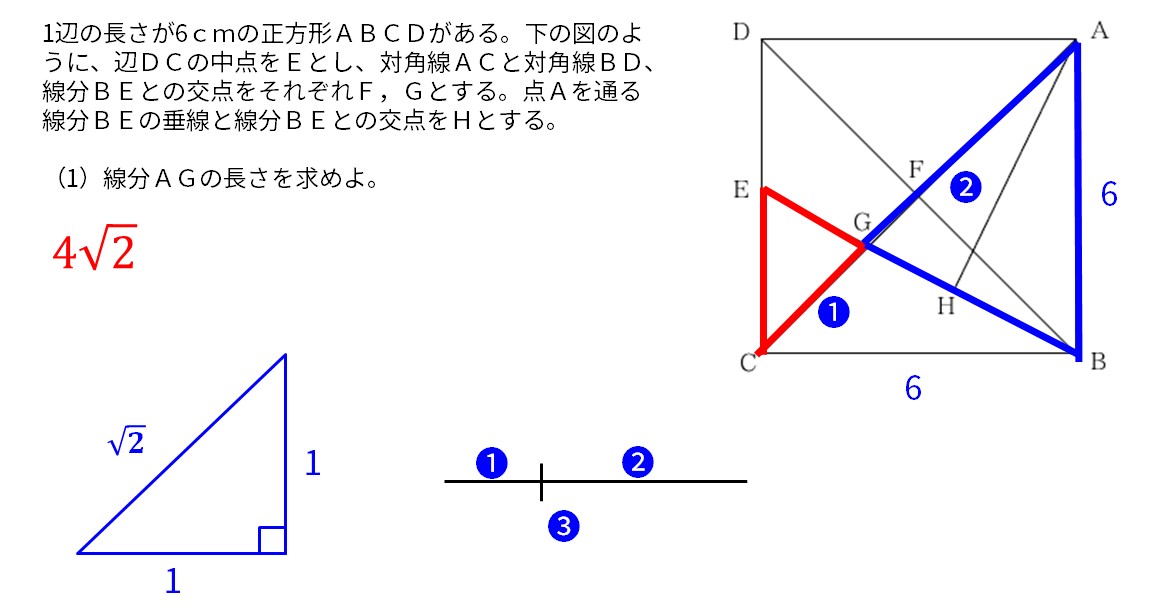
特別な直角三角形の1：1：√2を利用する。

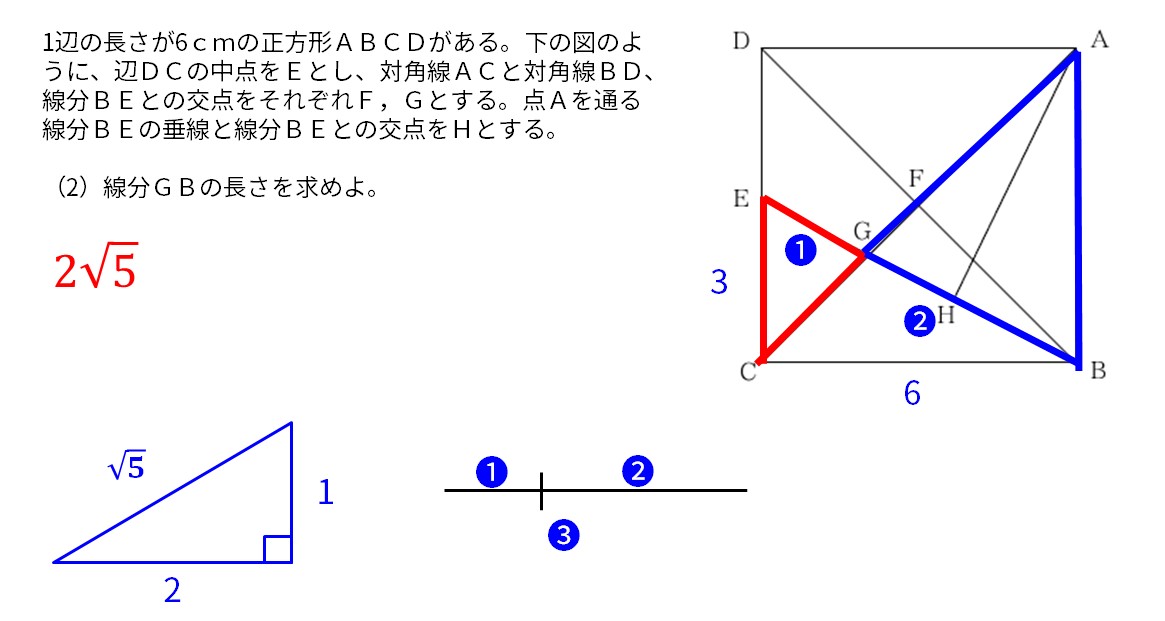
特別な直角三角形の1：2：√5を利用する。

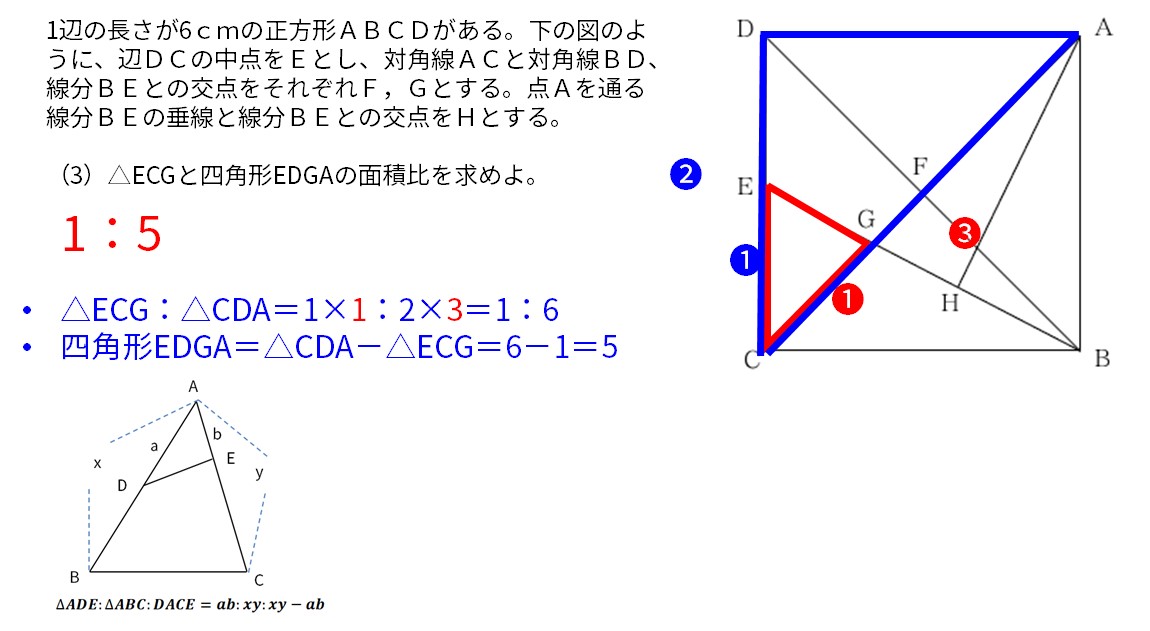
面積比を求めるテクニックの一つ、「共通する角があるときは、その角を挟む2辺の積が面積比になる」を活用。

△ECG：△CDA＝1×1：2×3＝1：6
四角形EDGA＝△CDA－△ECG＝6－1＝5

問5　空間図形

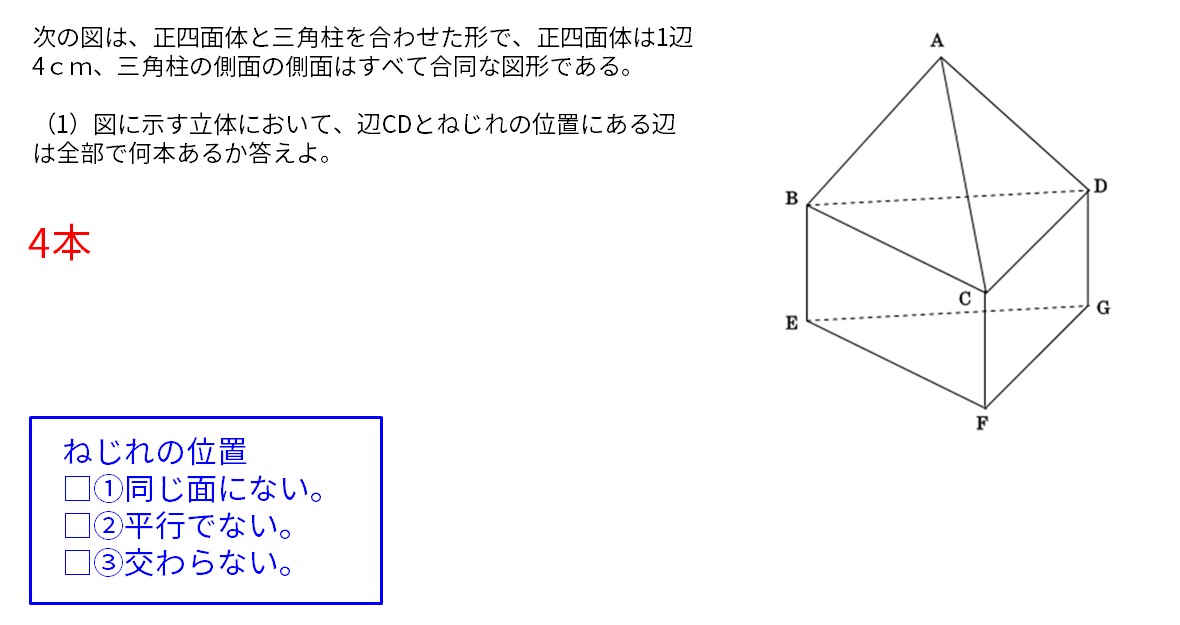
ねじれの位置は、
□①同じ面にない。
□②平行でない。
□③交わらない。
3つの「ない」がそろわないといけない。

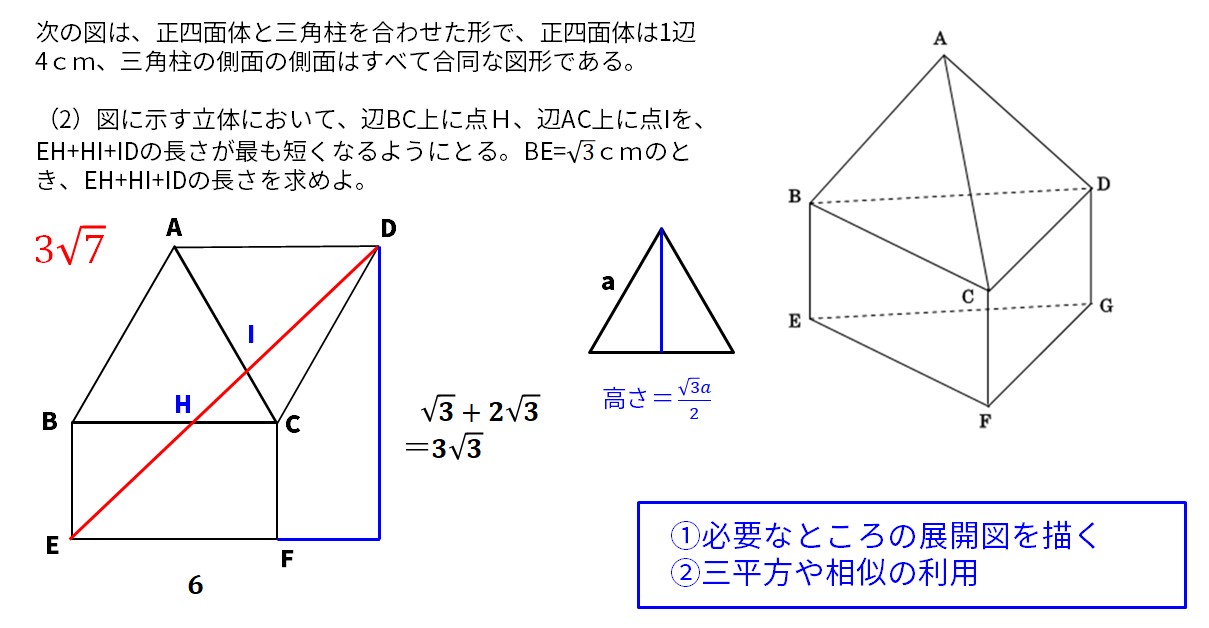
最短距離を求める手順は、
①必要なところの展開図を描く
②三平方や相似の利用

高校入試数学模擬応用問題（書き起こし）

問1
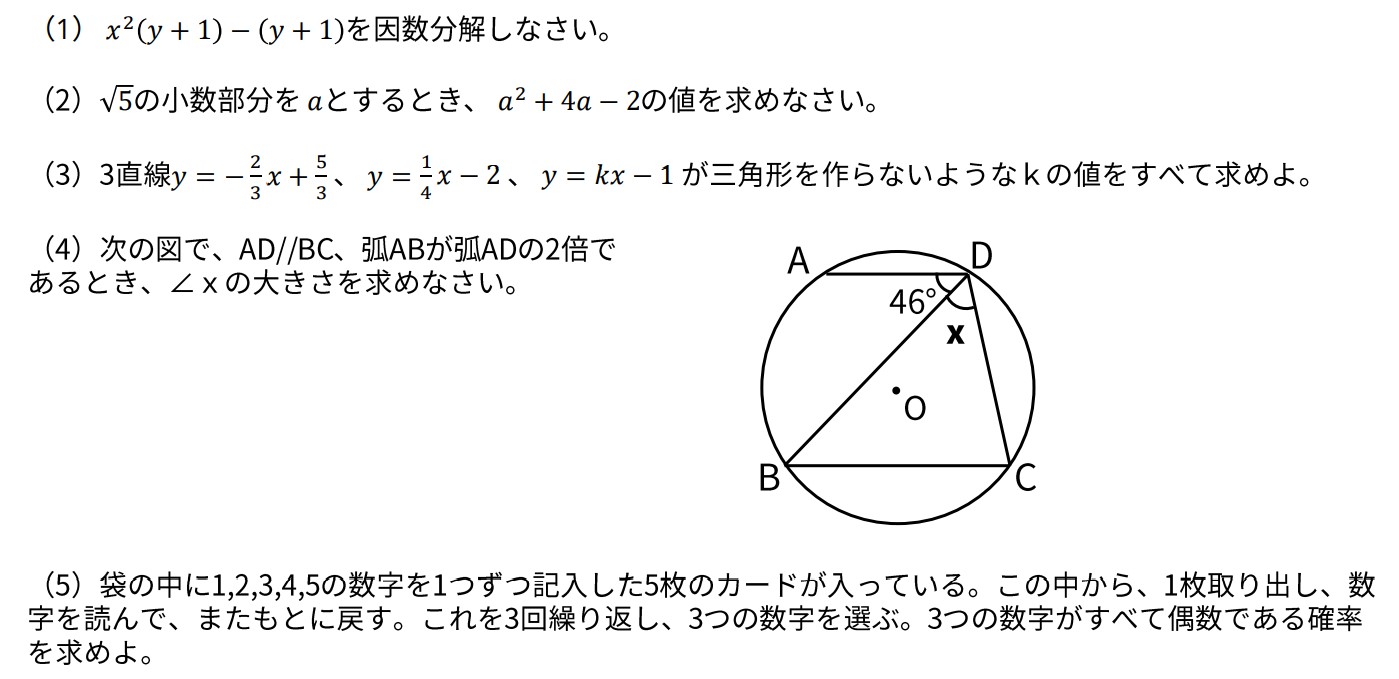
（1） 𝑥^2 (𝑦+1)−(𝑦+1)を因数分解しなさい。
（2）√5の小数部分を𝑎とするとき、 𝑎^2+4𝑎−2の値を求めなさい。
（3）3直線𝑦=−2/3 𝑥+5/3 、 𝑦=1/4 𝑥−2 𝑦=𝑘𝑥−1 が三角形を作らないようなｋの値をすべて求めよ。
（4）次の図で、AD//BC、弧ABが弧ADの2倍であるとき、∠ｘの大きさを求めなさい。
（5）袋の中に1,2,3,4,5の数字を1つずつ記入した5枚のカードが入っている。この中から、1枚取り出し、数字を読んで、またもとに戻す。これを3回繰り返し、3つの数字を選ぶ。3つの数字がすべて偶数である確率を求めよ。

問3
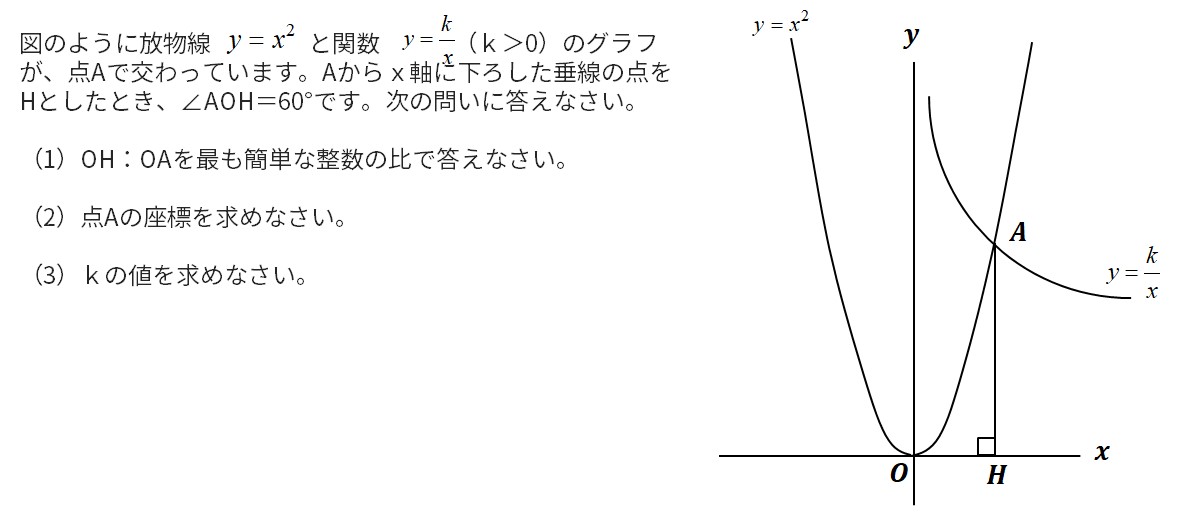
図のように放物線と関数（ｋ＞0）のグラフが、点Aで交わっています。Aからｘ軸に下ろした垂線の点をHとしたとき、∠AOH＝60°です。次の問いに答えなさい。
（1）OH：OAを最も簡単な整数の比で答えなさい。
（2）点Aの座標を求めなさい。
（3）ｋの値を求めなさい。

問4
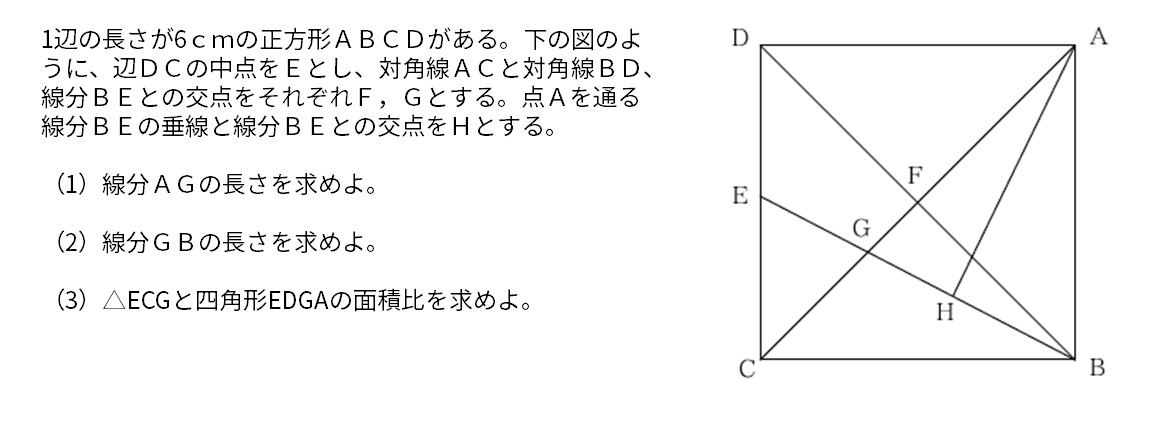
1辺の長さが6ｃｍの正方形ＡＢＣＤがある。下の図のように、辺ＤＣの中点をＥとし、対角線ＡＣと対角線ＢＤ、線分ＢＥとの交点をそれぞれＦ，Ｇとする。点Ａを通る線分ＢＥの垂線と線分ＢＥとの交点をＨとする。
（1）線分ＡＧの長さを求めよ。
（2）線分ＧＢの長さを求めよ。
（3）△ECGと四角形EDGAの面積比を求めよ。

問5
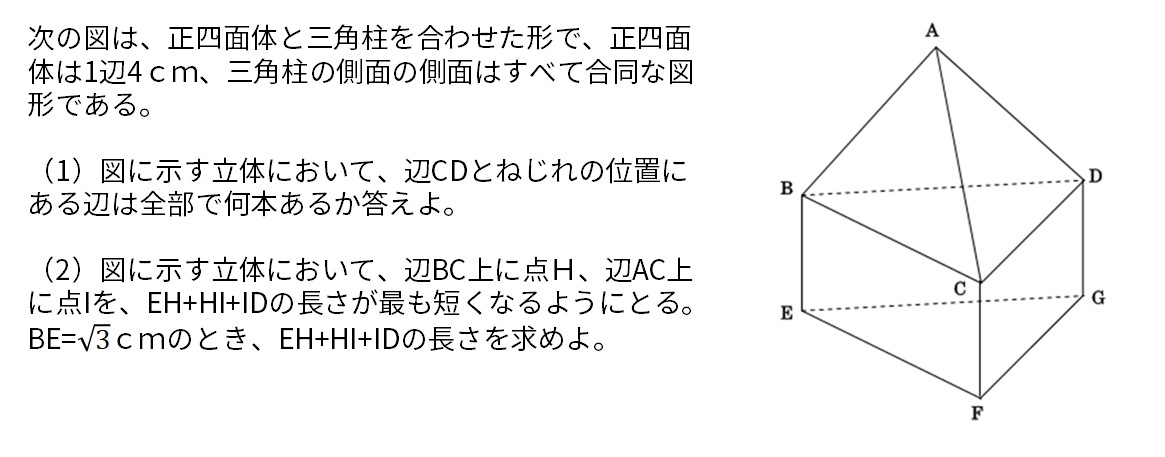
次の図は、正四面体と三角柱を合わせた形で、正四面体は1辺4ｃｍ、三角柱の側面の側面はすべて合同な図形である。
（1）図に示す立体において、辺CDとねじれの位置にある辺は全部で何本あるか答えよ。
（2）図に示す立体において、辺BC上に点Ｈ、辺AC上に点Iを、EH+HI+IDの長さが最も短くなるようにとる。BE=√3ｃｍのとき、EH+HI+IDの長さを求めよ。