中3数学「円周角の定理を使った証明・円周角を求める対策問題」

中3数学「円周角の定理を使った証明・円周角を求める対策問題」です。

■円周角と弧
弧の長さと円周角の大きさは、弧の長さに比例する。
つまり、

■円に内接する四角形と円周角
円に内接する四角形では、

■四角形の内接条件
次の1,2のどちらかが成り立つ四角形は、円に内接します。

■接線と弦のつくる角と円周角
円の接線とその接点を通る弦のつくる角の大きさは、その角の内部にある弧に対する円周角の大きさに等しい。（接弦定理）

■円周角

■円周角の定理

■円の直径に対する円周角の大きさ
円の直径に対する円周角の大きさは、90°である。

【問題】円周角の定理を使った証明・円周角を求める問題

【問1】

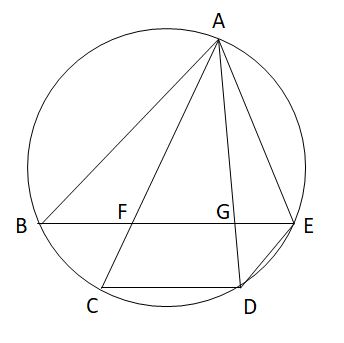
図のように、円Oの円周上に5点A,B,C,D,Eがある。BE//CDで、BE上にFとGがある。このとき、△ABG∽△EDGであることを証明せよ。

【問2】

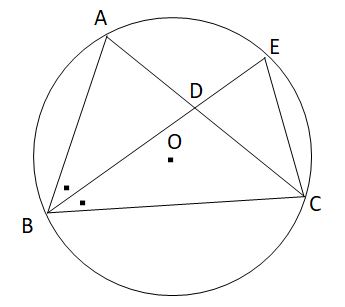
図のように、円Oの円周上に点A,B,Cを結んでできる△ABCがある∠ABCの二等分線と辺AC,円Oとの交点をそれぞれD,Eとする。このとき△DCE∽△CBEを証明しなさい。

【問3】

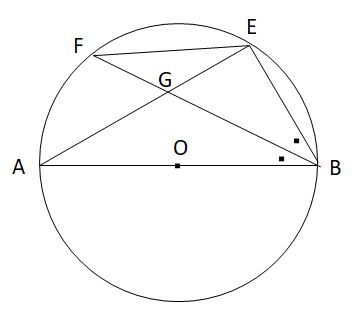
図は、線分ABを直径とする円Oがある。弧AB上に点Eをとり、∠ABEの二等分線と円O,線分AEとの交点をそれぞれF,Gとしたものです。このとき、△EFB∽△GFEであることを証明せよ。

【問4】次の図の、4点A,B,C,Dが同じ円周上にあることを証明しなさい。

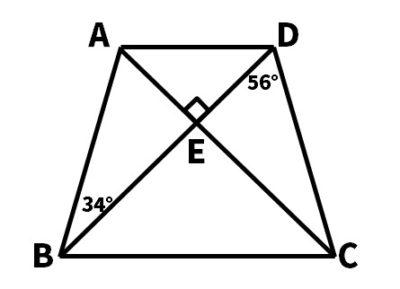
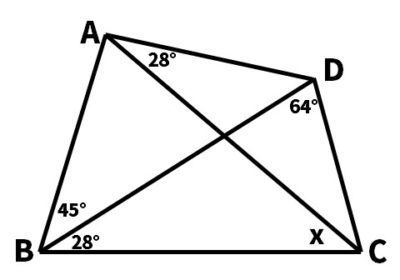
【問5】次の図で∠xの大きさを求めなさい。

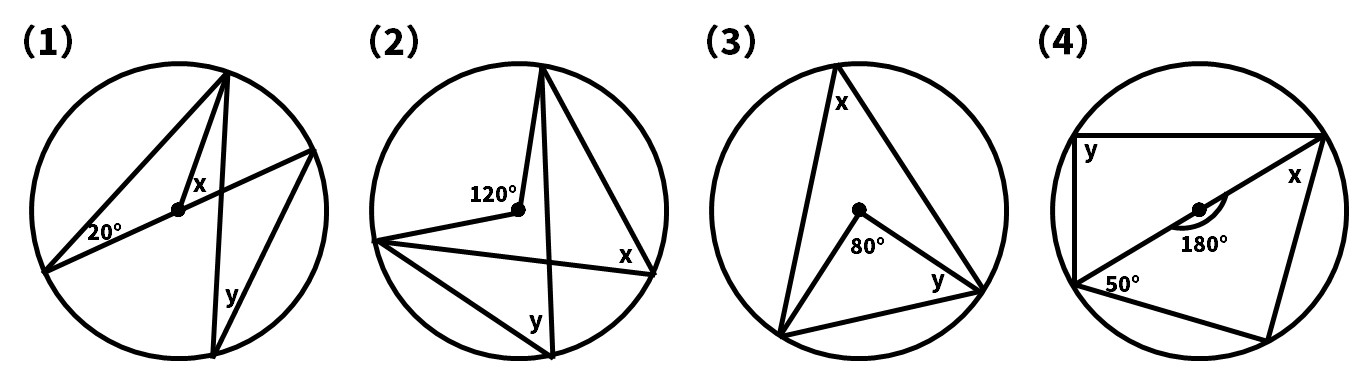
【問6】次の∠x、∠yの大きさを求めなさい。

【問1】
△ABGと△EDGにおいて、
対頂角より　∠AGB=∠EGD…①
弧BDに対する円周角より　∠BAG=∠DEG…②
①②より、2組の角がそれぞれ等しいので
△ABG∽△EDG

【問2】
△DCEと△CBEにおいて、
共通の角より　∠DEC=∠CEB…①
仮定より　∠CBE=∠ABD…②
弧AEに対する円周角より　∠DCE=∠ABD…③
②③より、∠CBE=∠DCE…④
①④より、2組の角がそれぞれ等しいので
△DCE∽△CBE

【問3】
△EFBと△GFEにおいて、
共通の角より　∠EFB=∠GFE…①
仮定より　∠EBF=∠ABF…②
弧AFに対する円周角より　∠GEF=∠ABF…③
②③より、∠EBF=∠GEF…④
①④より、2組の角がそれぞれ等しいので
△EFB∽△GFE

【問4】
図より、∠AEB=90°だから
∠BAE=90°-34°
=56°
したがって、∠BAE=∠BDC
よって、円周角の定理の逆より、
4点A,B,C,Dが1つの円周上にある。

【問5】43°

■円周角の定理の逆
点Ｐが直線ＡＢについて点Ｃと同じ側にあって、∠ＡＰＢ＝∠ＡＣＢならば、点Ｐは、3点Ａ，Ｂ，Ｃを通る円の周上にある。

■円と動点
円周角の定理の逆から、∠ＡＰＢが一定であるならば、点Ｐは円周上を動く。

【問6】
（1）∠x=40° ∠y=20°

（2）∠x=60° ∠y=60°

（3）∠x=40° ∠y=50°
∠yは、頂角80°の二等辺三角形の底角である（半径の長さは等しい）。よって、∠y=（180-80）÷2＝50

（4）∠x=40° ∠y=90°
直径の円周角は90°である。