中3数学「式の利用・整数の証明問題の定期テスト対策予想問題」

中3数学「整数の証明問題対策」についてです。

整数の証明問題対策1

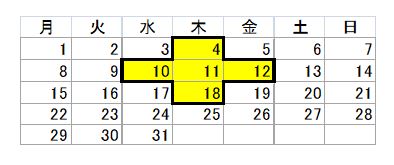
次の図は、ある年の8月のカレンダーである。カレンダーの中の5つの数を右の図のような形に囲んだら、どこを囲んでも、5つの数の和は、5の倍数であることを、囲んだ形の中央に位置する数をｎとして、証明せよ。

解答1

上の数は、ｎ－７　左の数は、ｎ－1　右の数は、ｎ＋1　下の数は、ｎ＋7と表せる。
ｎ＋（ｎ－7）＋（ｎ－1）＋（ｎ＋1）＋（ｎ＋7）＝5ｎ
ここで、ｎは、整数なので、5ｎは、5の倍数となる。

整数の証明問題対策2

連続する3つの整数のうち、最も小さい整数の2乗と最も大きい整数の2乗をたした数から2をひいた数は、真ん中の整数の2乗の2倍に等しいことを証明せよ。

解答2

整数ｎを使って、真ん中の数をｎとすると、連続する3つの整数は、（ｎ－1）、ｎ、（ｎ＋1）と表せる。

最も小さい整数の2乗と最も大きい整数の2乗をたした数から2をひいた数は
（ｎ－1）²+（ｎ－1）²－２
＝ｎ²－2ｎ+1＋（ｎ²＋2ｎ+1）－2
＝2ｎ²　　…①
真ん中の整数の2乗の2倍は、
ｎ²×2
＝2ｎ²　　…②
①②より最も小さい整数の2乗と最も大きい整数の2乗をたした数から2をひいた
数は、真ん中の整数の2乗の2倍に等しい

整数の証明問題対策3

2つの連続する偶数で、大きい方の偶数の平方から小さい方の偶数の平方をひくと、4の倍数となることを証明しなさい。

解答3

整数をnとすると、2つの連続する偶数を2n, 2n+2と表せる。
大きい方の偶数の平方から小さい方の偶数の平方をひくと、

(2n+2)²－(2n)²=4n²+8n+4－4n²
=8n+4
=4(2n+1)

nは整数なので2n＋1も整数となる。したがって2つの連続する偶数の平方の差は、4の倍数となる。

整数の証明問題対策4

3つの整数Ａ，Ｂ，Ｃがある。整数Ａは奇数で、整数Ｂは整数Ａより3だけ小さく、整数Ｃは整数Ａより4だけ大きい。このとき、整数Ａの2乗と整数Ｂと整数Ｃの和は、整数Ａより1だけ大きい数の2乗に等しくなることを証明せよ。

解答4

整数ｎを使って、整数Ａは2ｎ+1、整数Ｂは2ｎ-2、整数Ｃは2ｎ+5と表せる

整数Ａの2条と整数Ｂと整数Ｃの和は、
（2ｎ+1）²+（2ｎ-2）+（2ｎ+5）＝4ｎ²+8ｎ+4　…①

整数Ａより1だけ大きい数の2乗は
（2ｎ+1+1）²＝4ｎ²+8ｎ+4　…②

①②より、整数Ａの2乗と整数Ｂと整数Ｃの和は、整数Ａより1だけ大きい数の2乗に等しくなる。