▶ YouTube動画「トイトク」定期テスト・高校入試対策

中1数学「中学1年生で習う計算問題」ポイント解説付

2023.01.08
スポンサーリンク

中1数学「中学1年生で習う計算問題」をまとめています。定期テスト・実力テスト対策、日ごろの学習のお役立てください。

スポンサーリンク

中学1年生で習う計算問題

・0より小さい数
・正の数・負の数で量を表すこと
・絶対値と数の大小
・正の数・負の数の加法
・正の数・負の数の減法
・正の数・負の数の乗法
・正の数・負の数の除法
・乗法の計算法則
・加法と減法の混じった計算
・乗法と除法の混じった計算
・いろいろな計算（同じ数の積）
・文字式の表し方
・文字式の加法・減法
・文字式と数の乗法・除法
から構成されていまう。

【練習問題】0より小さい数

問1　次の問いに答えなさい。
（1）0℃とり2℃低い温度を-をつけて表しなさい。

問2　次の数を正の符号、負の符号をつけて表しなさい。
（1）0より10小さい数
（2）0より5大きい数

問3　次の数の中で、整数を答えなさい。
+0.2　+3　-1　0　+5　-3.9　+1/5

問4　-4　-1.5　+2を数直線上に表しなさい。
数直線の問題

【解答】
問1　次の問いに答えなさい。
（1）0℃とり2℃低い温度を-をつけて表しなさい。
-2℃

問2　次の数を正の符号、負の符号をつけて表しなさい。
（1）0より10小さい数　-10
（2）0より5大きい数　+5

  • 0より小さい数は「-」をつける
  • 0より大きい数は「+」をつける

問3　次の数の中で、整数を答えなさい。
+0.2　+3　-1　0　+5　-3.9　+1/5
（答え）+3　-1　0　+5

整数は

  • 正の整数（自然数）
  • 0
  • 負の整数

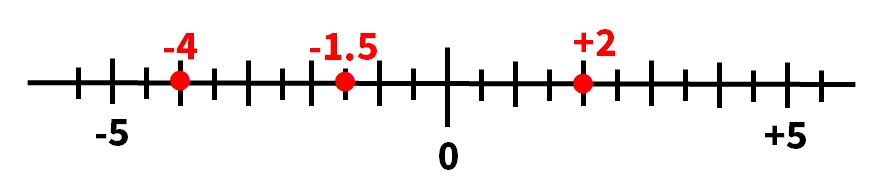
問4　-4　-1.5　+2を数直線上に表しなさい。
数直線の問題答え

【練習問題】正の数・負の数で量を表すこと

次の問いに答えなさい。

問1　「高い」と正の数で表すとき、次のことを表しなさい。
（1）4℃低い
（2）3℃高い

問2　【　　】内の言葉使って、次のことを荒しなさい。
（1）6個少ない【多い】

問3　次のことを、負の数を使わないで表しなさい。
（1）-8小さい

問4　60秒を基準として、次の5つの数を正の数・負の数を使って順に表しなさい。
57秒　61秒　70秒　35秒　88秒

【解答】
問1　「高い」と正の数で表すとき、次のことを表しなさい。
（1）4℃低い　-4℃
（2）3℃高い　+3℃

どちらを正の数で表すのかをしっかり読み取る。

問2　【　　】内の言葉使って、次のことを荒しなさい。
（1）6個少ない【多い】
（答）-6個多い

問3　次のことを、負の数を使わないで表しなさい。
（1）-8小さい
（答）8大きい

判定の性質をもつ量は、一方の言葉だけで表すことができる。

問4　60秒を貴人として、次の5つの数を正の数・負の数を使って順に表しなさい。
57秒　61秒　70秒　35秒　88秒
（答）-3秒　+1秒　+10秒　-25秒　+28秒

基準の量を決めて、増減や過不足を正の数、負の数で表す。

【練習問題】絶対値と数の大小

問1　次の問いに答えよ。

  1. +5の絶対値を求めよ。
  2. -5.1の絶対値を求めよ。
  3. 0の絶対値を求めよ。
  4. -2、5、0のうち最も絶対値が大きい数を求めよ。
  5. -7、6、4のうち最も絶対値が大きい数を求めよ。
  6. 1より5大きい数の絶対値を求めよ。
  7. -1より5大きい数の絶対値を求めよ。
  8. -3より1大きい数の絶対値を求めよ。
  9. 3より1大きい数の絶対値を求めよ。
  10. 2より-5小さい数の絶対値を求めよ。

問2　次の各組の数の大小を、不等号を使って表しなさい。
（1）3、　-6
（2）-15、　+14、　-13

【解答】
絶対値の説明図（中学）

  • 数直線と原点…数直線で0に対応する点を原点といいます。原点の右側に正の数を、左側に負の数を対応させます。また、右の方向を正の向き、左の方向を負の向きといいます。
  • 絶対値…数直線上で、ある数に対応する点から原点までの距離。正負の数から符号をとると、その数の絶対値になります。（例）+3の絶対値は、3。-4の絶対値は4です。

■数の大小
数の大小と数直線において、数直線上では、右にある数ほど大きく、左にある数ほど小さくなります。

  • 正の数は0より大きく、負の数は0より小さい。
  • 正の数は、絶対値が大きいほど大きい。
  • 負の数は、絶対値が大きいほど小さい。

■不等号
不等号は、数の大小を表す記号です。（小）＜（大）、（大）＞（小）

正の数・負の数

  • 正の数…0より大きい数。正の符号+（プラス）をつけて表します。
  • 負の数…0より小さい数。負の符号-（マイナス）をつけて表します。
  • 整数…負の整数、0、正の整数
  • 自然数…正の整数

※0は正の数、負の数でもありません。また符号+は、はぶくことができますが、-ははぶくことができません。たがいに反対の性質をもつと考えられる量は、一方を正の数、他方を負の数で表すことができます。（例）100ｇの増加を+100ｇとすれば、200ｇの減少は-200ｇと表されます。

問1

  1. 5
  2. 5.1
  3. 0
  4. 5
  5. -7
  6. 6
  7. 4
  8. 2
  9. 4
  10. 7

問2
（1）3＞-6
（2）-15＜-13＜+14

【練習問題】正の数・負の数の加法

次の問いに答えよ。

  1. （＋4）＋（＋2）を計算しなさい。
  2. （＋4）＋（＋4）を計算しなさい。
  3. （＋2）＋（＋8）を計算しなさい。
  4. （＋2）＋（＋1）を計算しなさい。
  5. （＋8）＋（＋9）を計算しなさい。
  6. （－4）＋（－2）を計算しなさい。
  7. （－4）＋（－4）を計算しなさい。
  8. （－2）＋（－8）を計算しなさい。
  9. （－2）＋（－1）を計算しなさい。
  10. （－8）＋（－9）を計算しなさい。
  11. （＋4）＋（－2）を計算しなさい。
  12. （＋4）＋（－4）を計算しなさい。
  13. （＋2）＋（－8）を計算しなさい。
  14. （＋2）＋（－1）を計算しなさい。
  15. （＋8）＋（－9）を計算しなさい。
  16. （－4）＋（＋2）を計算しなさい。
  17. （－4）＋（＋4）を計算しなさい。
  18. （－2）＋（＋8）を計算しなさい。
  19. （－2）＋（＋1）を計算しなさい。
  20. （－8）＋（＋9）を計算しなさい。

【解答】

加法のポイント

  • 同符号の2数の和…絶対値の和に、共通の符号をつけます。
  • 異符号の2数の和…絶対値の差に、絶対値が大きい方の符号をつけます。
  1. 6
  2. 8
  3. 10
  4. 3
  5. 17
  6. -6
  7. -8
  8. -10
  9. -3
  10. -17
  11. 2
  12. 0
  13. -6
  14. 1
  15. -1
  16. -2
  17. 0
  18. 6
  19. -1
  20. 1

【練習問題】正の数・負の数の減法

次の問いに答えよ。

  1. （＋4）－（＋2）を計算しなさい。
  2. （＋4）－（＋4）を計算しなさい。
  3. （＋2）－（＋8）を計算しなさい。
  4. （＋2）－（＋1）を計算しなさい。
  5. （＋8）－（＋9）を計算しなさい。
  6. （－4）－（＋2）を計算しなさい。
  7. （－4）－（＋4）を計算しなさい。
  8. （－2）－（＋8）を計算しなさい。
  9. （－2）－（＋1）を計算しなさい。
  10. （－8）－（＋9）を計算しなさい。
  11. （＋4）－（－2）を計算しなさい。
  12. （＋4）－（－4）を計算しなさい。
  13. （＋2）－（－8）を計算しなさい。
  14. （＋2）－（－1）を計算しなさい。
  15. （＋8）－（－9）を計算しなさい。
  16. （－4）－（－2）を計算しなさい。
  17. （－4）－（－4）を計算しなさい。
  18. （－2）－（－8）を計算しなさい。
  19. （－2）－（－1）を計算しなさい。
  20. （－8）－（－9）を計算しなさい。

【解答】

減法

  • ひく数の符号を変えて、加法になおして計算します。
  1. 2
  2. 0
  3. -6
  4. 1
  5. -1
  6. -6
  7. -8
  8. -10
  9. -3
  10. -17
  11. 6
  12. 8
  13. 10
  14. 3
  15. 17
  16. -2
  17. 0
  18. 6
  19. -1
  20. 1

【練習問題】正の数・負の数の乗法

次の計算をしなさい。

（1）（-7）×8
（2）（-5）×3
（3）4×（-1）
（4）5×（-9）
（5）12×（-10）
（6）11×（-4）
（7）（-2）×（-9）
（8）（-6）×（-8）
（9）（-8）×（-12）
（10）（-7）×（-7）

【解答】

2つの数の乗法（かけ算）

  • 同符号の2数の積…絶対値の積に、正の符号をつけます。
  • 異符号の2数の積…絶対値の積に、負の符号をつけます。

（1）（-7）×8
-56
（2）（-5）×3
-15
（3）4×（-1）
-4
（4）5×（-9）
-45
（5）12×（-10）
-120
（6）11×（-4）
-44
（7）（-2）×（-9）
18
（8）（-6）×（-8）
48
（9）（-8）×（-12）
96
（10）（-7）×（-7）
49

【練習問題】正の数・負の数の除法

次の計算をしなさい。

（1）（-12）÷3
（2）（-56）÷8
（3）30÷（-2）
（4）72÷（-9）
（5）（-55）÷（-5）
（6）（-98）÷-14）
（7）（-3.1）×0.6
（8）（-0.3）×0.5
（9）0÷（-1.6）
（10）（-7.5）÷（-1.5）

【解答】

2つの数の除法（わり算）

  • 同符号の2数の商…絶対値の商に、正の符号をつけます。
  • 異符号の2数の商…絶対値の商に。負の符号をつけます。
  • 逆数…2つの積が1のとき、一方の数を他方の数の逆数といいます。0の逆数はありません。（ある数の逆数をつくるには、符号はそのままにして、分母と分子を入れかえればいいです。）
  • 除法と逆数…ある数でわるには、その数の逆数をかければいいです。

（1）（-12）÷3
-4
（2）（-56）÷8
-7
（3）30÷（-2）
-15
（4）72÷（-9）
-8
（5）（-55）÷（-5）
11
（6）（-98）÷-14）
7
（7）（-3.1）×0.6
-1.86
（8）（-0.3）×0.5
0.15
（9）0÷（-1.6）
0
（10）（-7.5）÷（-1.5）
5

【練習問題】乗法の計算法則

  1. 2×18＋2×82を計算しなさい。
  2. （-2）×18＋（-2）×82を計算しなさい。
  3. 2×18＋2×22を計算しなさい。
  4. 2×52－2×42を計算しなさい。
  5. 5×42－5×22を計算しなさい。
  6. 18×2＋82×2を計算しなさい。
  7. 18×（-2）＋82×（-2）を計算しなさい。
  8. 18×2＋22×2を計算しなさい。
  9. 52×2－42×2を計算しなさい。
  10. 42×5－22×5を計算しなさい。

【解答】

計算の工夫

  • 計算の順序…累乗・（　　）の中⇒乗法・除法⇒加法・減法となります。
  • 交換法則や結合法則を使い、かける数の順序を組み合わせを変えて工夫しながら計算するといいでしょう。
  • 分配法則も使えます。
  1. 200
  2. -200
  3. 60
  4. 20
  5. 100
  6. 200
  7. -200
  8. 60
  9. 20
  10. 100

【練習問題】加法と減法の混じった計算

問1　次の式の正の項、負の項を答えなさい。
（1）5-10+21-4
（2）-3-5+13-21+4

問2　次の計算をしなさい。
（1）-9+12+8-13
（2）27-23+13-17
（3）0.8-45+3.1
（4）-2.6+5.9+6.2-0.8
乗除の計算問題
（7）（+2）-（+7）+（-4）
（8）（-13）-（+12）-（-9）+（+23）

【解答】

加法と減法の混じった計算

  • 減法をすべて加法になおし計算します。
  • かっこのない式になおし、正の項、負の項の和をそれぞれ求めて計算する

問1
（1）正の項　5　12　負の項　-10　-4
（2）正の項　13　4　負の項　-3　-5　-21

問2
（1）-2
（2）0
（3）-0.6
（4）8.7
（5）3/4
（6）-19/30
（7）-9
（8）7

【練習問題】乗法と除法の混じった計算

次の計算をしなさい。
（1）5×（-6）÷10
（2）（-4）×15÷5
（3）18×3÷（-9）
（4）（－20）×（-3）÷9
（5）（-96）÷2÷（-8）
（6）81÷（-3）÷9
乗除の計算問題

【解答】

3つ以上の数の乗法

  • 3つ以上の積…積の符号は負の数が奇数個のとき－、偶数個のとき＋。積の絶対値は、それぞれの数の絶対値の積となります。
  • 乗法と除法の混じった計算…乗法だけになおしたあと、席の符号を決めてから計算できる。

（1）-3
（2）-12
（3）-6
（4）-10
（5）6
（6）-3
（7）-4/9
（8）-1/8
（9）1/5
（10）5/9

【練習問題】いろいろな計算（同じ数の積）

次の問いに答えなさい。

  1. (－4)2を計算しなさい。
  2. (－3)2を計算しなさい。
  3. (－6)2を計算しなさい。
  4. (－9)2を計算しなさい。
  5. (－2)3を計算しなさい。
  6. －42を計算しなさい。
  7. －32を計算しなさい。
  8. －62を計算しなさい。
  9. －92を計算しなさい。
  10. －23を計算しなさい。
  11. (－3)2×4を計算しなさい。
  12. －32×4を計算しなさい。
  13. －32×22を計算しなさい。
  14. （－32）×22を計算しなさい
  15. （－32）×（-2）3を計算しなさい。
  16. (－4)2÷4を計算しなさい。
  17. －42÷4を計算しなさい。
  18. －42÷22を計算しなさい。
  19. （－42）÷22を計算しなさい。
  20. （－42）÷（-2）3を計算しなさい。

【解答】

累乗（指数）
同じ数を2個かけ合わせたものをその数の2乗、3個掛け合わせたものを3乗…といいます。2乗、3乗…その数の累乗といいます。かけあわせる個数をその数の右肩に小さく書きます。このことを指数といいます。とくに、2乗のことを平方、3乗のことを立方といいます。
  1. 16
  2. 9
  3. 36
  4. 81
  5. -8
  6. -16
  7. -9
  8. -36
  9. -81
  10. -8
  11. 36
  12. -36
  13. -36
  14. -36
  15. 72
  16. 4
  17. -4
  18. -4
  19. 4
  20. 2

【練習問題】文字式の表し方

次の式を、文字式の表し方にしたがって書きなさい。（×、÷を使わないで表しなさい。）

（1）x×y
（2）a×b×c
（3）x×x×y×y
（4）a÷4
（5）4x÷9
（6）(a-b)÷4
（7）a×3+b÷4
（8）(-1)×x-(-2)÷y
（9）x+x÷y
（10）3×(x-y)-z÷5

【解答】

文字式の表し方
・かけ算の記号（×）は省く。
・数と文字の積では、文字の前に数を書く。
・同じ文字の積は指数を使う。
・指数は、かけあわす数や文字の個数を示すことに注意する。
・わり算の記号（÷）を使わず、分数の形で書く。
・いらない（　）は省く。
・＋、－は省略できない。

（1）x×y
=xy

（2）a×b×c
=abc

（3）x×x×y×y
=x2y2

（4）a÷4
=a/4

（5）4x÷9
=4x/9

（6）(a-b)÷4
=a-b /4

（7）a×3+b÷4
=3a+b/4

（8）(-1)×x-(-2)÷y
=x+ 2/y

（9）x+x÷y
=x+x/y

（10）3×(x-y)-z÷5
=3(x-y)-z/5

【練習問題】文字式の加法・減法

次の問いに答えなさい。

  1. 2x－3－5x＋7を計算しなさい。
  2. 5x－3－2x＋6を計算しなさい。
  3. 3x＋2＋x－7を計算しなさい。
  4. 5x＋2＋4x－8を計算しなさい。
  5. 3x－3－4x－9を計算しなさい。
  6. 5x＋4＋3x－3を計算しなさい。
  7. (5x＋6)＋(2x－3)を計算しなさい。
  8. (6x＋6)－(3x－2)を計算しなさい。
  9. (－7x－10)＋(x＋6) を計算しなさい。
  10. (5x＋2)－(2x－6)を計算しなさい。

【解答】

必要な用語の確認です。

  • 項…文字式を加法だけでの式になおしたとき、加法の記号＋で結ばれたそれぞれの式や数をいいます。
  • 係数…文字を含む項の数の部分。
  • 1次式…2ｘ、5ｙのように、文字が1つだけの項を1次の項といいます。1次の項だけか、1次の項と数の項の和で表される式を1次式といいます。

計算の仕方

  1. 文字の部分が同じ項をまとめます。
  2. 1次式の加法・減法は、かっこをはずして分配法則をつかいます。
    ※加法は、そのままかっこをはずしますが。減法はひく方の式の各項の符号を変えてかっこをはずします。
  1. -3ｘ+4
  2. 3ｘ+3
  3. 4ｘ-5
  4. 9ｘ-6
  5. -ｘ-12
  6. 8ｘ+1
  7. 7ｘ+3
  8. 3ｘ+8
  9. -6ｘ-4
  10. 3ｘ+8

【練習問題】文字式と数の乗法・除法

次の計算をしなさい。
（1）5x×2
（2）(-3)×3x
（3）-5x×（-5）
（4）12x÷3
（5）-3x÷（-3）
（6）3(2x+6)
（7）-2(2x-5)
（8）(9x-12)÷3
（9）（-18x÷2）÷（-2）
（10）2(x+2)-4(5x-2)

【解答】

乗法・除法

  1. 項と数の積…文字の部分はそのままにし、数を係数にかけます。
  2. 1次式と数の乗法は、分配法則をつかって、かっこをはずします。
  3. 1次式の数の除法は、わる数を逆数にして乗法にして計算します。
・1次式と数の四則…分配法則を使ってかっこをはずし。文字の部分が同じ項をまとめます。
・式の値…式の中の文字を数でおきかえることを、文字にその数を代入するといい、代入して計算した結果をそのときの式の値といいます。

（1）5x×2
=10x

（2）(-3)×3x
=-9x

（3）-5x×（-5）
=25x

（4）12x÷3
=4x

（5）-3x÷（-3）
=x

（6）3(2x+6)
=6x+18

（7）-2(2x-5)
=-4x+10

（8）(9x-12)÷3
=3x-4

（9）（-18x÷2）÷（-2）
=9x+1

（10）2(x+2)-4(5x-2)
=-18x+12

コメント

テキストのコピーはできません。