中3数学「二次方程式の定期対策テスト問題」です。定期テスト対策として典型問題を解きましょう。復習や実力テスト対策にもご利用ください。
【対策問題】二次方程式
【問1 二次方程式を解く】次の方程式を解きなさい。
(1)7x2=63
(2)16x2-7=0
(3)(x-2)2=9
(4)(x+3)2=5
(5)(x-5)2=0
(6)(x+3)(x-4)=0
(7)x2+4x+3=0
(8)x2+2x-3=0
(9)x2-x-6=0
(10)x2-5x=0
(11)x2+12=7x
(12)x2=8x-16
(13)x2-6x+4=0
(14)x2-2x=48
(15)3(x+2)(x-2)=2x2-x
(16)(x-2)2=-x+8
(17)x2-2x-24=0
(18)x2+4x-12=0
【問2 二次方程式の文章題】
(1)連続した3つの自然数がある。その最小の数の平方は、残りの2数の和に等しくなります。最小の数をxとして、式をつくり連続する3つの自然数を求めなさい。ただし、途中の式も書きなさい。
(2)連続した3つの正の整数があり、最も大きい数の平方は他の2つの数の積の2倍より95小さい。このとき、この3つの数を求めよ。ただし、方程式を作り、求める途中の式も書け。
(3)連続する2つの奇数があり、小さい方の奇数を2乗して32を加えた数は,大きい方の奇数を9倍した数に等しい。このとき小さい方の奇数をxとして、xの値を求めよ。xの値を求める過程も、式と計算を含めて書け。
(4)大小2つの数があって、その差は8で、積は9になるという。大小2つの数を求めなさい。ただし、方程式を作り、求める途中の式も書け。
(5)大小2つの自然数がある。大きい数は小さい数より4大きく、この2つの数の積は、この2つの数の和を5倍した数より4小さい。大きい数と小さい数をそれぞれ求めなさい。途中式も書け。
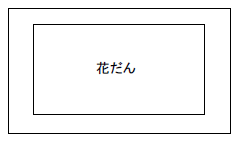
(6)図のように、縦10m、横20mの花だんのまわりに、同じ幅の歩道をつけたら、歩道の面積は400m2になりました。この道幅を求めなさい。ただし、方程式をつくり、求める過程も書け。
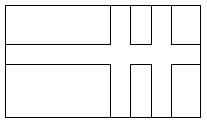
(7)図のような縦9cm,横16cmの長方形の土地に、縦と横に同じ幅の道をつくり、花だんを6つ作ったところ、6つの花だんの面積が長方形の土地の面積の7/12(12分の7)になりました。この道幅をxmとして、式をつくり道幅を求めなさい。ただし、途中の式も書きなさい。
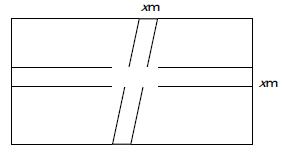
(8)縦が24m、横が35mの長方形の土地がある。図のように、長方形の各辺に面した部分がxmの道路をつけて、残りを畑にしたい。畑の面積が726m2になるようなxを求めなさい。途中式も書け。
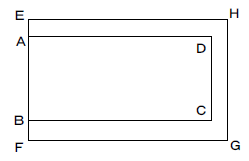
(9)次の図のように、2つの長方形ABCD、EFGHがあり、辺EF上に辺ABがあります。 AB=6cm、BC=8cmで、頂点Cから辺GHまでの距離は、AEの長さ、BFの長さと同じです。 図のコの字の部分の面積が長方形ABCDの面積の半分になるとき、 頂点Cから辺GHまでの距離は何cmになりますか。頂点Cから辺GHまでの距離をxcmとして方程式をつくり、求めなさい。
【解答・解説】二次方程式
■二次方程式を解き方
- 平方根の利用
- 因数分解の利用
- 平方完成の利用
- 解の公式の利用
以上4つの解き方があります。
| 解き方 | 例題 | ポイント |
| 平方根の利用 | x2=36 | x2の項と数字の方程式のときに使用 |
| 因数分解の利用 | x2+5x+6=0 | xの項があるときに使用。 |
| 平方完成の利用 | x2+6x-8=0 | 因数分解ができないときに使用 |
| 解の公式の利用 | x2+7x-8=0 | 因数分解ができない。さらにxの係数が奇数のときに使用。 |
平方根の利用の時、x2の係数が1以外の場合は、その係数で割ったり、くくるなりして方程式を整理してから解きます。
解の公式は、どの二次方程式を解く問題でも使用できますが、平方根や因数分解を利用できるときは、そちらで解いたほうがより早く、正確に答えを導けます。また、解の公式には、xの項が偶数のとき、より簡単な公式が存在します。
平方完成を利用するときは、xの係数が分数のときに、その威力がもっとも増します。
以上のように、二次方程式を解く問題には、4つの解法パターンがあるので、問題を数多くとき、慣れていきましょう。
【問1 二次方程式を解く】
(1)x=±3
(2)x=±√7/4
(3)x=-1,5
(4)x=3±√5
(5)x=5
(6)x=3、-4
(7)x=-1、-3
(8)x=1、-3
(9)x=-2,3
(10)x=0,5
(11)x=3,4
(12)x=4
(13)x=3±√5
(14)x=-6,8
(15)x=3,-4
(16)x=-1,4
(17)x=-4、6
(18)x=2、-6
【問2 二次方程式文章題】
(1)
x2=(x+1)+(x+2)
x=-1 、3
x=-1は問題に合わない。
(答え)3.4.5
(2)
真ん中の数をxとすると、(x-1)、x、(x+1)と表せる。
(x+1)2=2(x2-x)-95
x=-8 、12
x=-8は問題に合わない。
(答え)11.12.13
(3)
小さい方の奇数をxとおくと,大きい方の奇数はx+2となる。
したがってx2+32=9(x+2)
x=2,7
xは奇数よりx=2は不適
(答)xの値・・・7
(4)
小さい数をxとすると、大きい数は(x+8)と表せる。
x(x+8)=9
x=1 、-9
これは問題に合う。
(答)小さい数=1cmのとき、大きい数=9cm小さい数=-9cmのとき、大きい数=-1cm
(5)
x(x+4)=5(2x+4)-4
x=-2 、 8
x=-2は問題に合わない。
(答え)小8 大12
(6)
(10+2x)(20+2x)-200=400
x=5、-20
x=-20は問題に合わない。
(答え)5m
(7)
(9-x)(16-2x)=9×16×7/12
x=2 、15
x=15は問題に合わない。
(答え)2
(8)
(24-x)(35-x)=726
x=2 、57
x=57は問題に合わない。
(答え)2
(9)
(6+2x)(8+x)-48=24
x=1 、-12
x=--12は問題に合わない。
(答え)1cm

コメント