中3数学「3学期学年末テスト過去問対策問題」

中3数学「3学期学年末テスト過去問対策問題」です。過去問を分析して、対策問題を作成しています。

相似、三平方の定理を中心に、これまでの復習単元も網羅しています。

【問題】3学期学年末テスト過去問対策問題（中3数学）

問一　次の問いに答えなさい。

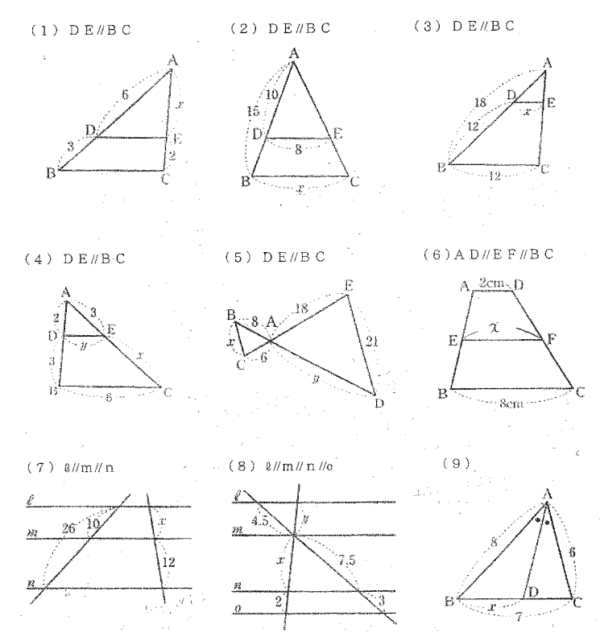
問二　次のx、yを求めなさい。

問三　次の図は、関数y=1/3×2…➀のグラフと、このグラフ上の2点A,Bを通る直線ℓを示したものです。2点A,Bのx座標はそれぞれ-6，3です。このとき、次の問いに答えなさい。

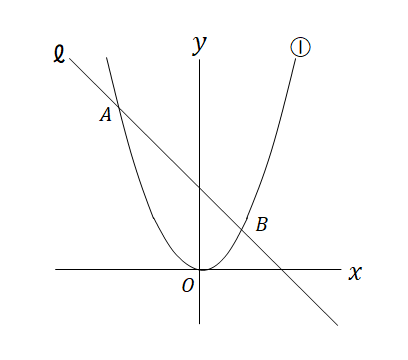
（1）点Aのy座標を求めなさい。
（2）直線ℓの傾きを求めなさい。

問四　下の図のように、点Oを中心とし、線分ABを直径とする半径5ｃｍの半円がある。弧AB上に、2点C,Dをとり、直線ACと直線BDの交点をEとする。また、線分ADと線分BCの交点をFとする。このとき、∠ABC＝15°、∠AEB＝45°である。次の問いに答えよ。

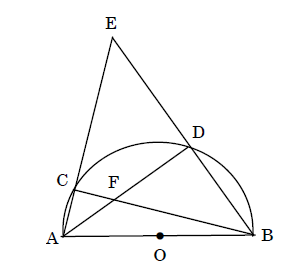
（1）△EAD∽△EBCを証明せよ。
（2）∠AFBは何度か、求めよ。
（3）弧ACと弧DBの長さの比を、最も簡単な整数の比で表せ。
（4）△ABEの面積を求めよ。

問一
（1）28
（2）-18
（3）7x-11/12 （12分の7x-11）　分母が12、分子が7x-11
（4）-1
（5）-√3
（6）x=5
（7）x=1、y=-3
（8）(x-6)(x+5)
（9）x=-7、x=13
（10）a=-1

問二
（1）x=4
（2）x=12
（3）x=4
（4）x=4.5 y=2.4
（5）x=7 y=24
（6）x=5
（7）x=7.5
（8）x=5 y=3
（9）x=4

問三
（1）12
（2）-1

問四
（1）△ＥＡＤと△ＥＢＣにおいて
∠ＥＤＡ＝∠ＥＣＢ＝90°（直径の円周角）…①
∠ＡＥＤ＝∠ＢＥＣ（共通な角）…②
①②より、2組の角がそれぞれ等しいので△EAD∽△EＢC

（2）△ＡＣＥが、直角二等辺三角形のことから∠ＥＡＤ=45°。直角三角形ＡＤＦの外角の定理（通称：スリッパの定理）より、135°

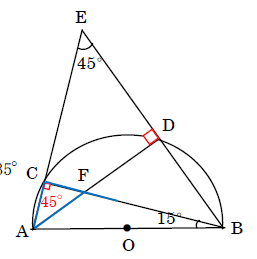
（3）弧の長さの比＝円周角の比（円周角は、弧の長さに比例する。）図示より、弧ACの円周角＝15°、弧DBの円周角＝30°より弧ACと弧DBの長さの比＝1：2

（4）△ABEの面積＝△ＡＤＥ+△ＡＢＤとなる。△ＡＢＤで、問題より、辺ＡＢ＝10ｃｍ、特別な直角三角形（1：2：√3 ）を利用して、