【中3数学】二次関数「点の移動」テスト対策｜よく出る問題パターンと解き方のコツを解説！

中学3年生の数学で学ぶ「二次関数の点の移動」は、定期テストでも入試でも頻出の重要単元です。「y=ax²のグラフ上の点がどのように動くか」「移動後の座標をどう求めるか」など、少し複雑な問題も出題されやすいため、しっかりとパターンを押さえておく必要があります。この記事では、よく出る問題の解き方や、つまずきやすいポイントを丁寧に解説します。得点源にしたい人はぜひチェックしておきましょう！

二次関数の点の移動に関するテスト対策問題（中3数学）

図の△AOBにおいて、点PはAから0へ動き、点QはBから0へ動くとします。そこで、2点P、QがA、Bをそれぞれ同時にスタートし、また、点P (秒速xcm)は点Qの半分の速さで動くとしてつぎの各問について答えなさい。ただし、OA=12cm、OB=24cmとする。

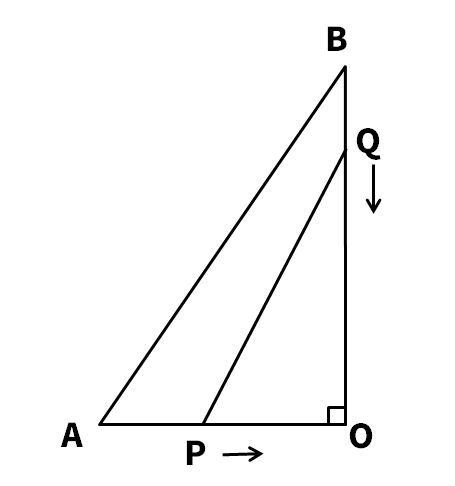
(1) スタートして4秒後に△POQの面積が16cmになった。このときの点Pの速さを求めなさい。

(2) 点Pが秒速3cmのとき、 t秒後に△POQの面積が9cm²になった。つぎの問いに答えなさい。
①tの変域を求めなさい。
②POQの面積が9cm²になったのは何秒後ですか。

二次関数の点の移動に関するテスト対策問題（中3数学）の解答・解説

（1） 秒速2cm
(12-4x) (24 – 8x) ×1/2=16
x=3±1
x=2, 4
ここでx=4であると、点Pは3秒で点0まで着いてしまうので、 4秒後
という問題の条件から不適。
よって、x=2 だから

（2）
①0≦t≦4

②3秒後
(12-3t) (24-6t) ×1/2=9
t=4±1
t=3, 5
よって、①より、 t = 5は不適。
ゆえに t = 3 だから
3秒後