中2数学「平面図形の角度を求める定期対策テスト問題」です。
【対策問題】平面図形の角度を求める
【問1 対頂角・同位角・錯角】
(1)
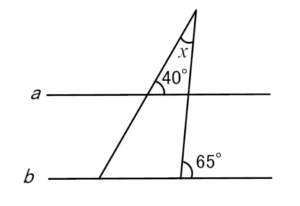
a//bのとき、∠xを求めよ。
(2)
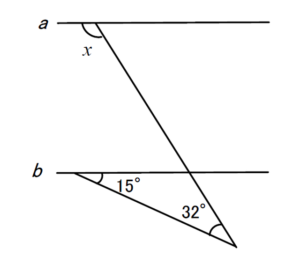
a//bのとき、∠xを求めよ。
【問2 対頂角・同位角・錯角➋】
次の図のように直線l、mに、直線nが交わっています。次の角を答えなさい。
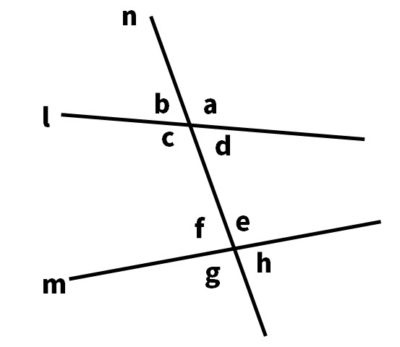
(1)∠aの同位角
(2)∠cの錯角
【問3 三角形の内角と外角】
(1)次の図で∠x、∠yの大きさを求めなさい。
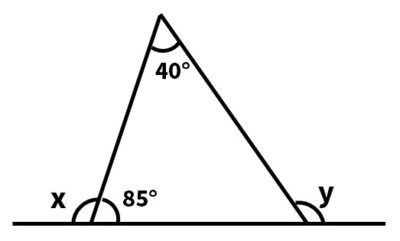
(2)次の問いに答えよ。
- △ABCで∠A=40°、∠B=80°のとき△ABCは何という三角形か。
- △ABCで∠A=30°、∠B=40°のとき△ABCは何という三角形か。
- △ABCで∠A=40°、∠B=50°のとき△ABCは何という三角形か。
- △ABCで∠A=45°、∠B=45°のとき△ABCは何という三角形か。
- △ABCで∠A=30°、∠B=80°のとき△ABCは何という三角形か。
- △ABCで∠A=50°、∠B=20°のとき△ABCは何という三角形か。
- △ABCで∠A=60°、∠B=30°のとき△ABCは何という三角形か。
- △ABCで∠A=55°、∠B=35°のとき△ABCは何という三角形か。
- △ABCで∠A=20°、∠B=70°のとき△ABCは何という三角形か。
- △ABCで∠A=120°、∠B=30°のとき△ABCは何という三角形か。
【問4 多角形の内角の和】
次の問いに答えなさい。
(1)十角形の内角の和を求めなさい。
(2)内角の和が900°となるのは何角形ですか。
(3)1つの内角の大きさが144°である正多角形の内角の和を求めよ。
(4)1つの内角と1つの外角のそれぞれの大きさが、7:2になっているのは正何角形ですか。
(5)正n角形で、1つの内角の大きさが1つの外角の大きさの8倍になっているとき、nの値を求めなさい。
(6)次の図の∠xの大きさを求めなさい。
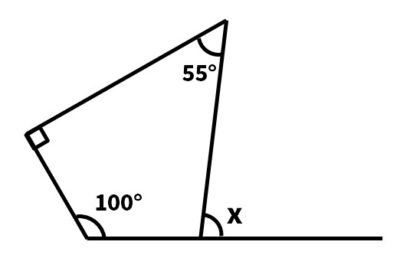
【問5 多角形の外角の和】
次の問いに答えなさい。
- 正六角形の1つの外角の大きさを求めなさい。
- 1つの外角の大きさが30°になるのは、正何角形ですか。
- 正十角形の1つの内角を求めなさい。
- 1つの内角の大きさが120°である正多角形の1つの外角の大きさを求めよ。
- 1つの外角の大きさが40°である正多角形を求めよ。
【解答・解説】平面図形の角度を求める
【問1 対頂角・同位角・錯角➊】
(1)25°
(2)133°
■同位角・錯角
- 2つの直線に1つの直線が交わるとき、2つの直線が平行ならば、同位角と錯覚は等しくなります。
- 2つの直線に1つの直線が交わるとき、同位角か錯覚が等しいならば、2つの直線は平行になります。
【問2 対頂角・同位角・錯角➋】
(1)∠e
(2)∠e
■平行線と角
ビジュアル(図)で覚えておくといいです。×型が対頂角、F型が同位角、クロス型が錯角のイメージですね。同位角は、錯角は、いつでも等しい角になるわけでなく、平行の2直線であればという条件がつくことをお忘れなく。直線で交わってできる向かいあった角のことを対頂角といいます。対頂角は等しくなります。

➊∠aと∠c、∠dと∠h、∠bと∠f、∠cと∠yのような位置にある2つの角を同位角という。
➋∠cと∠e、∠dと∠fのような位置にある2つの角を錯角という。
【問3 三角形の内角と外角】
(1)
∠x=95°
∠y=125°
(2)
- 鋭角三角形
- 鈍角三角形
- 直角三角形
- 直角二等辺三角形
- 鋭角三角形
- 鈍角三角形
- 直角三角形
- 直角三角形
- 直角三角形
- 二等辺三角形
■三角形
- 三角形の内角の性質…三角形の内角の和は180°です。
- 三角形の外角の性質…三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。
■鋭角・鈍角
- 鋭角…0°より大きく90°より小さい角を鋭角といいます。
- 鈍角…90°より大きく180°より小さい角を鈍角といいます。
■三角形の種類
- 鋭角三角形…3つの内角がすべて鋭角である三角形
- 直角三角形…1つの内角が直角である三角形
- 鈍角三角形…1つの内角で鈍角である三角形
【問4 多角形の内角の和】
(1)1440°
(2)七角形
(3)1440°
(4)九角形
(5)十八角形
(6)65°
内角の和=180(n-2)°■1つの内角
1つの内角=180° -1つの外角(となりあう外角と内角は180°)です
■内角と外角
△ABCと辺BCを延長した直線上の点をDとします。このとき、∠ACDを頂点Cにおける外角といいます。辺ACを延長してできる∠BCEも頂点Cにおける外角となります。外角に対して、△ABCの3つの角∠A、∠B、∠Cを内角といいます。
■三角形の角度
- 三角形の3つの内角の和=180°
- 三角形の1つの外角は、そのとなり合わない2つの内角の和に等しくなります。
【問5 多角形の外角の和】
- 60°
- 十二角形
- 144°
- 60°
- 九角形
■(正)n角形の角度の公式
- 内角の和=180(n-2)°
- 外角の和=360° (多角形の外角の和は、辺の数にかかわらず360°)です。
- 1つの内角+1つの外角=180° (となりあう外角と内角は180°)です。
- 1つの外角=360÷n
- 1つの内角=180°-1つの外角=180°-(360/n)
■対角線の本数
- 対角線の本数=n(n-3)/2(本)となることも覚えておきましょう。
【豆知識】対頂角・同位角・錯角が等しい理由
対頂角が等しいことの証明
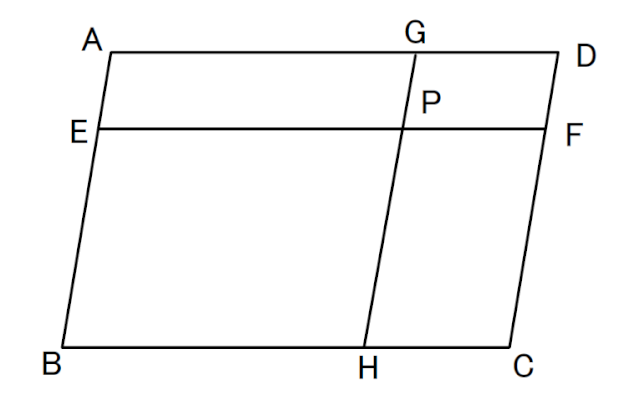
∠GPE=100°のとき
∠GPE=∠FPH=100°
また、
∠EPH=180°-∠GPE
=180°-100°
=80°
よって、
∠GPF=∠EPH=80° (対頂角は等しい)
同位角が等しいことの証明

∠AEPと∠EBHや∠GPFと∠PHCのような位置関係にある角を同位角といいます。EF//BCのとき、∠AEP=∠EBHや∠GPF=∠PHCとなります。
同位角は等しいのでなく、2直線が平行であれば、同位角は等しくなるということを覚えておきましょう。
錯角が等しいことの証明

∠AGPと∠GPFや∠EPHと∠PHCのような位置関係にある角を錯角といいます。AD//EF//BCのとき、∠AGP=∠GPFや∠EPH=∠PHCとなります。

コメント