高校入試対策・数学「度数分布表を利用した連立方程式文章題」についてまとめています。近年、出題か見られるようになった形式の1つです。しっかり慣れておきましょう。それでは、高校入試対策・数学「度数分布表を利用した連立方程式文章題」です。
度数分布表を利用した連立方程式文章題1
次の表は、あるクラスの生徒22人の通学時間を度数分布表にまとめたものである。この表から通学時間の平均値を求めたところ、20分となった。このとき、x、yにあてはまる数を連立方程式を立式し求めよ。
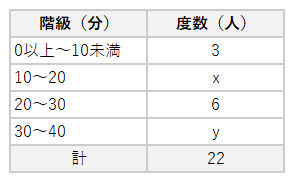
度数分布表(通学時間)
解答1
x=9 y=4
(解説)
3+x+6+y=22…①
15+15x+150+35=440…②
の連立方程式を解く。
度数分布表を利用した連立方程式文章題2
次の表は、ある中学校の男子の体重を測定してつくった度数分布表で、度数が2か所欠けている。階級値44 kgで表される階級値の相対度数は、階級値36 kgで表される階級値の相対度数より0.06大きい。このとき、階級値44 kgで表される階級の度数を求めなさい。ただし、階級値36kgの度数をx、階級値44kgをyとし連立方程式を作り、求めるまでの過程を書き求めよ。
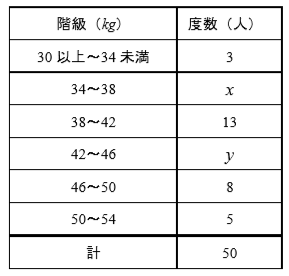
度数分布表(体重)
解答2
x+y=21
-2x+2y=6
これを解くと、x=9 y=12これは問題に合う。よって、12
度数分布表を利用した連立方程式文章題3
次の表は、A中学校の3年生のあるクラスが、古本を集めた結果を度数分布表に整理したものである。このクラスが集めた古本の重さの平均値は8kgになりました。このとき、4kg以上8kg未満の階級の度数をx人、8kg以上12kg未満の階級の度数をy人とし、連立方程式をつくって、それぞれの階級の度数を求めよ。
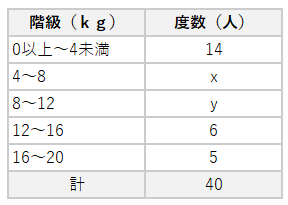
度数分布表(古本)
解答3
x=8 y=7
(解説)
14+x+y+6+5=40
28+6x+10y+84+90=320
これを解く。

コメント