中１理科「地震の計算練習問題」

中１理科の「地震の計算練習問題」についてまとめています。

地震の計算問題（基礎）

1. 震源からの距離が48kmの場所で、地震が発生してから8秒後に地面がゆれ始めた。このときのP波の速さは何km/sか。
2. 震源から45km離れたA地点では初期微動が6時48分57秒に始まり、震源から200km離れたB地点では初期微動が6時49分22秒に始まった。このとき、初期微動を伝える波の速さは何km/sか。
3. ある地震で、震源から50km離れたA地点の初期微動継続時間が6秒であったとき、震源から120km離れたB地点の初期微動継続時間は何秒か。

地震の計算（基礎）解答

1. 48km÷8s=6km/s
2. A地点とB地点の震源からの距離の差は200-45=155km。初期微動の到着時刻の差は25秒より155km÷25s=62km/s
3. 初期微動継続時間は震源距離に比例するので、B地点の初期微動継続時間をx秒すると、50km:6秒=120km:x秒。よって、x=14.4秒

地震の計算問題（標準）

下のグラフは、ある地震の2つの波が伝わる速さを記録したものである。次の各問いに答えなさい。

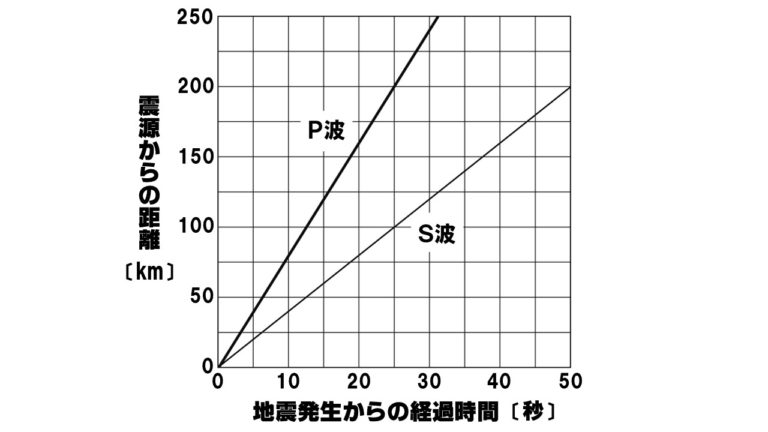
1. 初期微動継続時間が25秒になるのは、震源からの距離が何kmの地点か。
2. 震源からの距離が320km地点での初期微動継続時間は何秒になるか。
3. 震源から100km離れた地点にS波が到着した時刻は16時15分40秒であった。この地震の発生時刻は何時何分何秒か。

地震の計算（標準）解答

1. 200km （解説）グラフより、P波が到着してからS波が到着するまでの時間差が25秒になっているのは200km地点になっています。
2. 40秒 （解説）震源からの距離と初期微動継続時間は比例するので、200km：25秒＝320km：ｘ秒。これを解くとｘ＝40秒 16時15分15秒
3. 16時15分40秒ー25秒＝16時15分15秒 （解説）グラフより、100km地点にS波が到着したのは地震が発生してから25秒後だとわかる。つまり100km地点にS波が到着した時刻の25秒前に地震が発生したとわかる。

地震の計算問題（応用）

ある地震について、2つの波が到着した時刻と震源からの距離の関係を調べたところ次のグラフのようになりました。次の問いに答えよ。

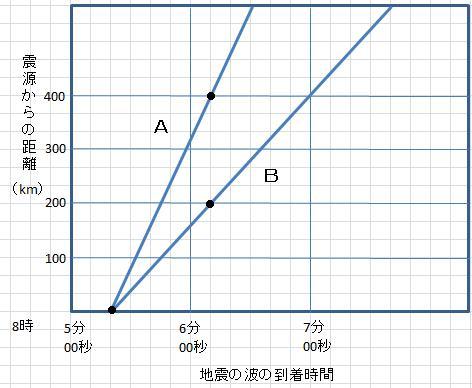
1. グラフから、この地震が発生した時刻は、何時何分何秒か求めよ。
2. Ｐ波のグラフは、Ａ，Ｂのどちらか答えよ。
3. Ｂの波の伝わる速さを求めよ。
4. 震源からの距離が200kmの地点での初期微動が始まった時刻を求めよ。
5. 震源からの距離が200kmの地点での初期微動継続時間は何秒か求めよ。

地震の計算（応用）解答

1. 8時5分20秒
2. Ａ
3. 4km/s　（200÷5＝4）
4. 8時5分45秒
5. 25秒

関連中１理科「地震の学習ポイント」