中学3年生の数学で扱う「二次関数と三角形の面積比」は、関数と図形の知識を組み合わせて考える応用力が問われる重要単元です。放物線と直線が囲む図形の面積や、x軸・y軸との交点を活用した三角形の面積比を求める問題は、定期テストや入試でもよく出題されます。この記事では、二次関数のグラフ上にできる三角形の面積や比の求め方、よくあるミスや計算のコツなどを丁寧に解説。図形問題で差をつけたい中学生は必見です!
二次関数「三角形の面積比に関するテスト対策問題(中3数学)
図のように、直線と放物線y=x2、y軸、x軸との交点をA、B、C、Dとする。このとき、つぎの各問いに答えよ。
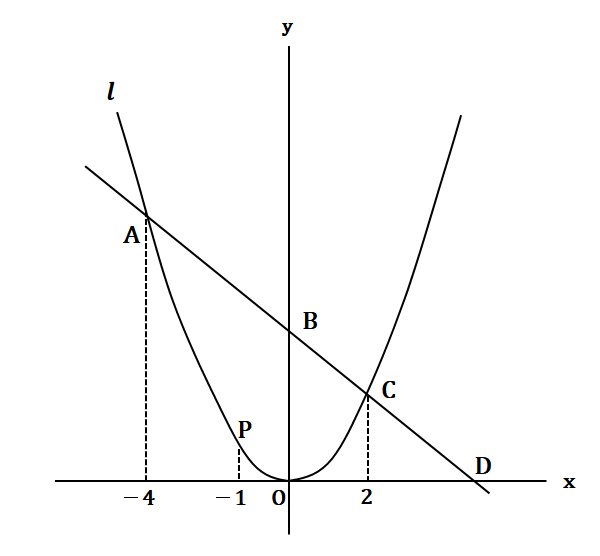
(1)点Aの座標を求めなさい。
(2)直線の式を求めなさい。
(3)点Pを通り、△OACの面積を2等分する直線の式を求めなさい。
(4)△CAPと△COPの面積比を求めなさい。
二次関数「三角形の面積比に関するテスト対策問題(中3数学)の解答・解説
(1) A(-4, 16)
点A、Cは各 x 座標を放物線の式に代入し、点A(-4, 16)、C(2,4)。この2点より、直線の式は、y=-2x+8 これより、点Bは切片ゆえ、B(0, 8)。また、点Dはx軸との交点ゆえ、y=0を代入。D(4,0) 。したがって、A(-4, 16)
(2) y=-2x+8
(3) y= 4x+8
まず、点Pを求めたいので 直線 OAの式y=axに点Aの座標を代入し、y=-4x。点Pの座標は、x座標が-1より、P(-1,4)。辺OAに対する頂点Cと点Pを結んだ線分と平行で、辺OAの中点Mを通る直線と辺ACの交点をQとする。するとこの点QとPを結んだ直線が△OACの面積を2等分する。そこで、2点P(-1, 4) C(2,4) の座標より、線分PCはx軸に平行である。だから、辺OAの中点の座標 M(-2, 8)より、点Mからx軸に平行な直線をひくと、辺ACとの交点は点B (切片)と一致!求めたい交点QとBが一致。
したがって、点PとBを結んだ直線が△OACを2等分する。 2点P(-1,4) B(0, 8) を通る直線は、y=ax+8 とおけ、点Pを代入し、ついに求めたい直線の式が現れる。
(4) 3:1
△CAPと△COPはそれぞれ底辺をAP、OPとすると高さが共通。よって「(面積比)=(底辺の比)」。
△CAP:△COP=QP:RO = (-1- (-4)): (0-(-1))=3:1



コメント