高1数学「1学期定期テスト（数Ⅰ）過去問分析問題」高校数学準備にも

高1数学「1学期定期テスト（数Ⅰ）過去問分析問題」です。高校数学準備にもお役立てください。

1学期定期テスト（数Ⅰ）問題一覧

・次数と係数
・乗法の公式の利用
・不等式
・分母の有理化と式の値
・2次方程式の判別式
から構成しています。

次数と係数

問1　xについて考えるとき、次の単項式の次数と係数を答えなさい。
（1）3x²
（2）-6x⁴
（3）-x³y
（4）-3a²bx³

問2　次の整式はxについて何次式か。また、各項の係数、および定数項を求めなさい。
（1）2x²+x+4
（2）-x³-6x²+3
（3）x²+2ax+a²
（4）3x³y-5xy²-7y³

問3　整式-x³+2x²y-3y²について、次の問いに答えなさい。
（1）xについて何次式か。また、各項の係数、および定数項を求めなさい。
（2）yについて何次式か。また、各項の係数、および定数項を求めなさい。

次数と係数の解答

問1
（1）次数…2　係数…3
（2）次数…4　係数…-6
（3）次数…3　係数…-y
（4）次数…3　係数…-3a²b

問2
（1）2次式　x²の係数…2　xの係数…1　定数項…4
（2）3次式　x³の係数…-1　x²の係数…-3　定数項…3
（3）2次式　x²の係数…1　xの係数…2a　定数項…a²
（4）3次式　x³の係数…3y　xの係数…-5y²　定数項…-7y³

問3
（1）3次式　x³の係数…-1　x²の係数…2y　定数項…-3y²

（2）2次式　y²の係数…-3　yの係数…2x²　定数項…-x³

乗法の公式の利用

問1　次の式を展開しなさい。

（1）(a-b+c)²
（2）(x+y-2z)²
（3）(a-b-c)²

（4）(x²+xy+y²)(x²-xy+y²)
（5）(a+b+c)(a+b-c)
（6）(3x-y-1)(3x-y+1)
（7）(a²-a+2)(a²-a-2)

（8）(x+2)(x-2)(x²+4)
（9）(x-3)(x+3)(x²+9)
（10）(x+y)(x-y)(x²+y²)(x⁴+y⁴)

（11）(x+3)³
（12）(x+2)(x²-2x+4)
（13）(3a-b)(9a²+3ab+b²)

乗法の公式の利用の解答

（1）(a-b+c)²

a-bをAとすると
(A+c)²
=A²+2Ac+c²
=(a-b)²+2(a-b)c+c²
=a²-2ab-b²+2ac-2bc+c²
=a²+b²+c²-2ab-2bc+2ca

（2）(x+y-2z)²
=x²+y²+4z²+2xy-4yz-4zx

（3）(a-b-c)²
=a²+b²+c²-2ab+2bc-2ca

（4）(x²+xy+y²)(x²-xy+y²)

(A+xy)(A-xy)
=A²-(xy)²
=(x²+y²)²-(xy)²
=x⁴+2x²y²+y⁴-x²y²
=x⁴+x²y²+y⁴

（5）(a+b+c)(a+b-c)
=a²+b²-c²+2ab

（6）(3x-y-1)(3x-y+1)
=9x²-6xy+y²-1

（7）(a²-a+2)(a²-a-2)
=a⁴-2a³+a²-4

（8）(x+2)(x-2)(x²+4)

=(x²-4)(x²+4)
=x⁴-16

（9）(x-3)(x+3)(x²+9)
=(x²-9)(x²+9)
=x⁴-81

（10）(x+y)(x-y)(x²+y²)(x⁴+y⁴)
=(x²-y²)(x²+y²)(x⁴+y⁴)
=(x⁴-y⁴)(x⁴+y⁴)
=x⁸-y⁸

（11）(x+3)³

=x³+9x²+27x+27

（12）(x+2)(x²-2x+4)

=x³+8

（13）(3a-b)(9a²+3ab+b²)
=27a³-b³

不等式

問1　次の不等式を解きなさい。
（1）-7x＜14

（2）2(x+4)＞5(x-2)

問2　不等式5x-7≧2x+9を満たす自然数をすべて求めよ。

問3　次の問いに答えなさい。
（1）ある1桁の自然数を2倍にして14をたした数は、もとの数から2を引いて5倍した数より小さくなる。もとの数を求めなさい。

（2）ある博物館の入館料は1人350円ですが、30人以上の団体なら1人の入館料が25％引きなる。30人以上より少ない人数でも30人の団体として入館した方が安くなるのは、何人以上のときか、求めなさい。

（3）1個250円のおにぎりと、1個150円のお茶を合わせて15個買い、代金を3000円以下にしたい。おにぎりをできるだけ多く買うとすると、おにぎりは何個まで買うことができるか、求めなさい。

問4　次の連立不等式を解きなさい。
・2x+3≧x-1…①
・x-2＞3x-4…②

不等式の解答

問1　次の不等式を解きなさい。
（1）-7x＜14
x＞-2

（2）2(x+4)＞5(x-2)
x＜6

問2　不等式5x-7≧2x+9を満たす自然数をすべて求めよ。
x≦16/3=5.33……
よって、不等号を満たす自然数は、1．2．3．4．5である。

問3　次の問いに答えなさい。
（1）ある1桁の自然数を2倍にして14をたした数は、もとの数から2を引いて5倍した数より小さくなる。もとの数を求めなさい。

もとの数をxとすると、条件より
2x+14<5(x-2)

2x+14<5x-10

-3<-24

x>8

この不等式を満たす1けたの自然数は9である。

（2）ある博物館の入館料は1人350円ですが、30人以上の団体なら1人の入館料が25％引きなる。30人以上より少ない人数でも30人の団体として入館した方が安くなるのは、何人以上のときか、求めなさい。

x人入館とする。
350x>350×（1-0.25）×30
x>30・(1-0.25)
x>22.5

この不等式を満たす最小の自然数は23である。
よって、23人以上のとき安くなる。

（3）1個250円のおにぎりと、1個150円のお茶を合わせて15個買い、代金を3000円以下にしたい。おにぎりをできるだけ多く買うとすると、おにぎりは何個まで買うことができるか、求めなさい。

おにぎりをx個買うとき、お茶は(15-x）個買うことになる。

250x+150(15-x)≦3000
250x+2250-150x≦3000
100x≦750
x≦7.5

この不等式を満たす最大の整数は7である。
よって、7個までおにぎりを買うことができる。

問4　次の連立不等式を解きなさい。
・2x+3≧x-1…①
・x-2＞3x-4…②

①を解くと、x≧-4
②を解くと、x＜1

よって、-4≦x＜1

分母の有理化と式の値

式の分母を有理化と式の値を求める問題です。

分母の有理化と式の値の解説・解答

問1
（1）√15+2√3
（2）5+2√6

問2
（1）6
（2）1
（3）198

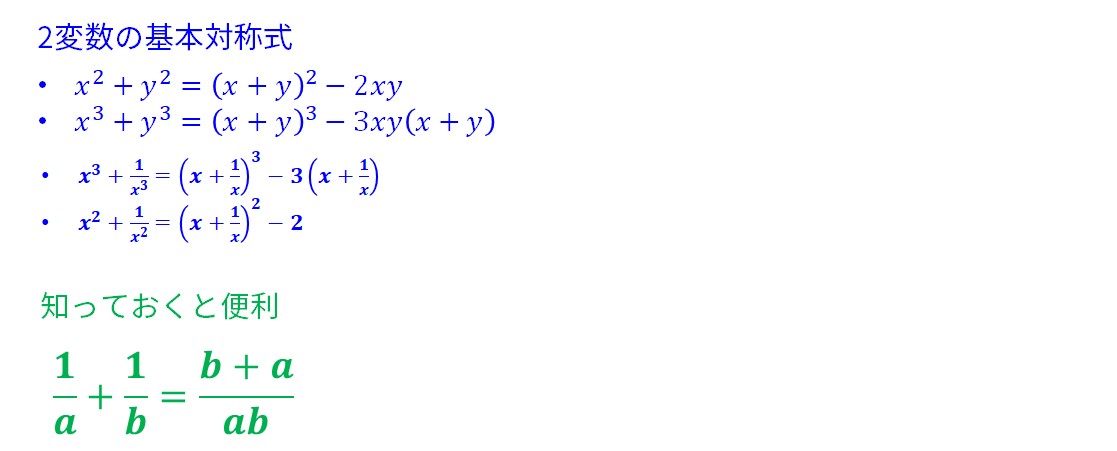
2次方程式の判別式

問1　次の2次方程式の実数解の個数を求めよ。
（1）x²+5x-2=0
（2）x²+x+1=0

問2　2次方程式x²-mx-m+8=0が重解をもつとき、定数mの値を求めよ。

問3　2次方程式x²-2x+m=0が異なる2つの実数解をもつとき、定数mの値の範囲を求めよ。

問4　正方形の土地がある。この土地の縦の長さを3m、横の長さを6m長くすると、元の面積の3倍になった。元の土地の面積を求めよ。

2次方程式の判別式の解答

問1　次の2次方程式の実数解の個数を求めよ。
（1）x²+5x-2=0
2次方程式の判別式D＝33>0より、
2個

（2）x²+x+1=0
2次方程式の判別式D＝-3<0より、
0個

問2　2次方程式x²-mx-m+8=0が重解をもつとき、定数mの値を求めよ。
重解をもつのは、2次方程式の判別式D＝0より
D=(-m)²-4・1・（-m+8)=0
m²-4m-32＝0
(m+8)(m-4)=0
m=-8,4

問3　2次方程式x²-2x+m=0が異なる2つの実数解をもつとき、定数mの値の範囲を求めよ。
異なる実数解をもつのは、2次方程式の判別式D>0より
D=(-2)²-4・1・m>0
4-4m>0
-4m>-4より
m<1

問4　正方形の土地がある。この土地の縦の長さを3m、横の長さを6m長くすると、元の面積の3倍になった。元の土地の面積を求めよ。

元の土地の1辺の長さをxmとする。

縦を3m、横を6m長くすると、土地の面積は(x+3)(x+6)
題意より、(x+3)(x+6)=3x²
これを解くと、x=-3/2、6
x>0であるから、x=6

よって、元の土地の面積は36m²となる。