中学数学「確率の練習問題」です。定期テスト対策として、典型問題を解いて本番に備えよう。
確率の練習問題一覧
・場合の数
・2つのさいころを投げたときの確率
・硬貨を投げたときの確率
・くじを引くときの確率
・2枚のカードの組を取り出す確率
についての対策テストとなっています。
【対策問題】場合の数
次の問いに答えなさい。
- 1つのさいころを1回投げるとき、起こりうる場合は全部で何通りあるか。
- 1つのさいころを1回投げるとき、6の約数の目が出る場合は何通りあるか。
- 1つのさいころを1回投げるとき、6の約数の目が出る確率を求めなさい。
- 1から20までの数を1つずつ記入した20枚のカードを1枚ひくとき、ひいた数が4の倍数である場合は何通りであるか。
■場合の数と確率
起こりうる場合が、すべてでn通り(=場合の数)あり、そのどれが起こることも同様に確からしいとする。ことがらAの起こる場合がn通りあるとき、Aの起こる確率pはp=a/nとなります。つぎに、「同様に確からしい」ということをみていきましょう。
起こりうる場合が、すべてでn通り(=場合の数)あり、そのどれが起こることも同様に確からしいとする。ことがらAの起こる場合がn通りあるとき、Aの起こる確率pはp=a/nとなります。つぎに、「同様に確からしい」ということをみていきましょう。
■同様に確からしい
さいころの目の出方は、1から6までの6通りあり、どの目が出ることも同じ程度に期待されます。このようなとき、どの目が出ることも同様にに確からしいといいます。
さいころの目の出方は、1から6までの6通りあり、どの目が出ることも同じ程度に期待されます。このようなとき、どの目が出ることも同様にに確からしいといいます。
【解答】
- 6
- 4
- 2/3
- 5
【対策問題】2つのさいころ
次の問いに答えよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の数が同じになる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の和が4になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の積が6になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の和が3の倍数になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の積が奇数になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の和が13 になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、出る目の和が7 になる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、a-b=1となる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、aとbの差が2となる確率を求めよ。
- 2個のサイコロa,b を同時に投げるとき、2a=bとなる確率を求めよ。
■サイコロの確率の求め方
2つのサイコロを投げて求める確率や、1つのサイコロを連続2回の確率の問題では、『表』を利用して、該当するところにチェックを入れて解いていくのが一般的です。もちろん、樹形図を利用して解いてもかまいません。
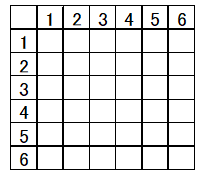
2つのサイコロを投げて求める確率や、1つのサイコロを連続2回の確率の問題では、『表』を利用して、該当するところにチェックを入れて解いていくのが一般的です。もちろん、樹形図を利用して解いてもかまいません。

■サイコロの場合の数
サイコロをn回振ったときの場合の数は、6nとなります。たとえば、サイコロを3回降ると、63=6×6×6=216通りとなります。
サイコロをn回振ったときの場合の数は、6nとなります。たとえば、サイコロを3回降ると、63=6×6×6=216通りとなります。
■ことがらAの起こらない確率
ことがらAの起こる確率をPとすると、Aの起こらない確率=1-P
ことがらAの起こる確率をPとすると、Aの起こらない確率=1-P
■2つのさいころを同時に投げるときの例題
2つのさいころを同時に投げるとき、次の確率をもとめなさい。
2つのさいころを同時に投げるとき、次の確率をもとめなさい。
- 出る目の数の和が10になる確率。
- 出る目の数の和が10以上になる確率
- 出る目の数の和だ10以上にならない確率
(解説・解答)
2つのさいころを、A,Bとすると、目の出方は6×6=36通り。
- 表を使って、出る目の和が10になるところを印をいれていくと、3通りある。よって、3/36=1/12が答えとなります。
- 表を使って、出る目の和が10以上にになるところを印をいれていくと、6通りある。よって、6/36=1/6が答えとなります。
- 2の答えを利用して、(10以上になる確率)+(10以上にならない確率)=1なので、1-1/6=5/6が答えとなります。
【解答】
- 1/6
- 1/12
- 1/9
- 1/3
- 1/4
- 0
- 1/6
- 5/36
- 2/9
- 1/12
【対策問題】硬貨
次の問いに答えよ。
- 2枚のコインを同時に投げるとき、2枚とも表になる確率を求めよ。
- 2枚のコインを同時に投げるとき、2枚とも裏になる確率を求めよ。
- 2枚のコインを同時に投げるとき、1枚が裏になる確率を求めよ。
- 2枚のコインを同時に投げるとき、少なくとも1枚が裏になる確率を求めよ。
- 3枚の硬貨を同時に投げるとき、3枚とも表になる確率を求めよ。
- 3枚の硬貨を同時に投げるとき、3枚とも裏になる確率を求めなさい。
- 3枚の硬貨を同時に投げるとき、1枚が表になる確率を求めなさい。
- 3枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
- 4枚の硬貨を同時に投げるとき、4枚とも表になる確率を求めよ。
- 4枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
■コイン・硬貨の確率の求め方
コイン・硬貨の確率は、『樹形図』を用いて解いていくのが一般的です。
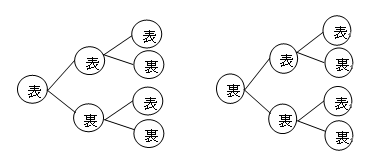 たとえば、2つのコインは、4通り 3つのコインの場合は、8通りとなる。
たとえば、2つのコインは、4通り 3つのコインの場合は、8通りとなる。
コイン・硬貨の確率は、『樹形図』を用いて解いていくのが一般的です。
 たとえば、2つのコインは、4通り 3つのコインの場合は、8通りとなる。
たとえば、2つのコインは、4通り 3つのコインの場合は、8通りとなる。
■コイン・硬貨の場合の数
樹形図を書いていくとわかりますが、コイン・硬貨の場合の数は、n回投げるとき、n2となります。4回投げると、24=16通りとなります。
樹形図を書いていくとわかりますが、コイン・硬貨の場合の数は、n回投げるとき、n2となります。4回投げると、24=16通りとなります。
■コイン・硬貨の確率の例題
3枚のコイン(硬貨)を同時に投げる時、2枚が表で、1枚が裏の出る確率を求めよ。(解説・解答)

樹形図より、場合の数は、8通りで、2枚が表で、1枚が裏となるのは3通りなので、答えは、3/8となります。
3枚のコイン(硬貨)を同時に投げる時、2枚が表で、1枚が裏の出る確率を求めよ。(解説・解答)

樹形図より、場合の数は、8通りで、2枚が表で、1枚が裏となるのは3通りなので、答えは、3/8となります。
【解答】
- 1/4
- 1/4
- 1/2
- 3/4
- 1/8
- 1/8
- 3/8
- 7/8
- 1/16
- 15/16
【対策問題】くじ
次の問いに答えよ。
- 当たりが2本、はずれが3本入っているくじがある。このくじを同時に2本ひくとき、2本とも当たりである確率を求めよ。
- 当たりが2本、はずれが3本入っているくじがある。2本ともはずれである確率を求めよ。
- 当たりが2本、はずれが3本入っているくじがある。少なくとも1本は当たりである確率を求めよ。
- 当たりが3本、はずれが2本入っているくじがある。このくじを同時に2本ひくとき、2本とも当たりである確率を求めよ。
- 当たりが3本、はずれが2本入っているくじがある。このくじを同時に2本ひくとき少なくとも1本は当たりである確率を求めよ。
- 6本中に当たりが3本入っているくじがある。このくじをまずAが引いて次にBが引くとき、Aが当たる確率を求めよ。
- 6本中に当たりが3本入っているくじがある。このくじをまずAが引いて次にBが引くとき、AがはずれてBが当たる確率を求めなさい。
- 6本中に当たりが3本入っているくじがある。このくじをまずAが引いて次にBが引くとき、AもBも当たる確率を求めなさい。
- 6本のうち、2本の当たりが入っているくじがある。この6本のくじの中から、同時に2本のくじをひくとき、1本だけ当たりである確率を求めよ。
- 2本の当たりくじが入っている5本のくじがある。このくじを,先にAさんが1本引き,これをもどさずに,次にBさんが1本引くとき,AさんとBさんのうち,どちらか1人が当たりくじを引く確率を求めよ。
■くじの確率の求め方
樹形図が基本でしょう。その際には、「辞書的に配列して行う」とわかりやすいと思います。たとえば以下のようになります。5本のうち、2本があたりのくじがある。ときたら、あたりくじ a,b はずれくじ c,d,eとアルファベット(辞書的)に配列して樹形図を書く。2本の当たりをa,bとし、残りをc,d,e,fとする。そうすると樹形図は、
樹形図が基本でしょう。その際には、「辞書的に配列して行う」とわかりやすいと思います。たとえば以下のようになります。5本のうち、2本があたりのくじがある。ときたら、あたりくじ a,b はずれくじ c,d,eとアルファベット(辞書的)に配列して樹形図を書く。2本の当たりをa,bとし、残りをc,d,e,fとする。そうすると樹形図は、
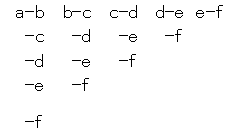
1本だけ当たりは、a-c a-d a-e a-f b-c b-d b-e b-fの8通り
上の樹形図より、場合の数は、15通りで、1本だけ当たりであるのは8通りなので、8/15となる。
【解答】
- 1/10
- 3/10
- 7/10
- 3/10
- 9/10
- 1/2
- 3/10
- 1/5
- 8/15
- 3/15
【対策問題】カード
次の問いに答えなさい。
- 1から4までの4つの数字が書かれたカードがそれぞれ1枚ずつある。このうち2枚を取り出して、2けたの数を作るとき2けたの整数が偶数になる確率を求めよ。
- 1から4までの4つの数字が書かれたカードがそれぞれ1枚ずつある。このうち2枚を取り出して、2けたの数を作るとき2けたの整数が30 より小さい確率を求めよ。
- 1から4までの4つの数字が書かれたカードがそれぞれ1枚ずつある。このうち2枚を取り出して、2けたの数を作るとき2けたの数が4の倍数になる確率を求めよ。
- 1から4までの4つの数字が書かれたカードがそれぞれ1枚ずつある。このうち2枚を取り出して、2けたの数を作るとき2けたの数が3の倍数になる確率を求めよ。
- 2,4,5,7,9の5枚のカードから2枚を引くとき2枚の数の和が11になる確率を求めよ。
- 2,4,5,7,9の5枚のカードから2枚を引くとき2枚の数の積が偶数になる確率を求めよ。
- 2,4,5,7,9の5枚のカードから2枚を引くとき2枚の数の和が偶数になる確率を求めよ。
- 2,4,5,7,9の5枚のカードから2枚を引くとき2枚の数の和が10以下になる確率を求めよ。
- 0、1、2、3、4、5の数字が1つずつ書かれた6枚のカ-ドから、同時に2枚を取り出すとき、取り出した2枚のカ-ドに書かれている数の積が0となる確率を求めよ。
- 1から6までの数字が1つずつ書かれた6個のボールが袋の中に入っている。袋からボールを一度に2個取り出すとき、書かれた数の和が8である確率を求めよ。
■カードの確率の求め方
大きく4つのパターンがあります。順番が関係する(数字をつくる)=「順列」、順番が関係ない(数字をつくらない)=「組み合わせ」に注視しましょう。・「1回戻し」+「数字を作る」
・「1回戻し」+「数字は作らない」
・「同時または続けて」+「数字を作る」
・「同時または続けて」+「数字を作らない」
大きく4つのパターンがあります。順番が関係する(数字をつくる)=「順列」、順番が関係ない(数字をつくらない)=「組み合わせ」に注視しましょう。・「1回戻し」+「数字を作る」
・「1回戻し」+「数字は作らない」
・「同時または続けて」+「数字を作る」
・「同時または続けて」+「数字を作らない」
【解答】
- 1/2
- 1/2
- 1/4
- 1/3
- 1/5
- 7/10
- 2/5
- 2/5
- 1/3
- 2/15

コメント