中2数学「後期中間対策テスト問題」よく出る問題を徹底解説！

中2数学「後期中間対策テスト問題」よく出る問題を徹底解説！です。後期中間テストが近づいてきましたね。今回のテスト範囲は「一次関数」が中心。直線の式の求め方やグラフの描き方、変化の割合、応用問題など、数学の基礎となる重要な内容が含まれています。

「傾きや切片を求めるのが苦手…」「グラフを正しく描けるか不安…」「文章題の式の立て方が難しい…」と感じている人もいるかもしれません。でも、ポイントを押さえて問題演習をすれば、確実に得点できる単元です！この記事では、テストによく出る問題を厳選し、解き方のコツをわかりやすく解説します。しっかり復習して、テスト本番に自信を持って挑みましょう！

テスト	範囲
中1数学前期中間	正負の数・指数計算・四則計算
中1数学前期期末	一次方程式
中1数学後期中間	比例反比例
中1数学後期期末	平面・空間図形・資料の整理
中2数学前期中間	文字式の計算
中2数学前期期末	連立方程式
【今回】中2数学後期中間	一次関数
中2数学後期期末	図形の性質と証明・確率
中3数学前期中間	展開・因数分解・平方根
中3数学前期期末	二次方程式
中3数学後期中間	二次関数
中3数学後期期末	相似・三平方の定理
※テスト範囲が違うときは、上記を参照にリンク先へ

後期中間対策テスト問題（中2数学）

後期中間対策テスト問題（中2数学）

【対策問題】一次関数であるもの

次のうち、yがxの一次関数であるものには○、そうでないものには×を書きなさい。

（1）毎分50Lの割合でプールに水を入れるとき、x分後のプールにたまった水yL
（2）40円の鉛筆をx本と60円の消しゴムを買ったときの代金y円
（3）1辺の長さがxcmの正方形の面積ycm²

【解答】

一次関数は一般的にy=ax+b（a,bは定数）で表される。b=0のとき、y=axとなり、比例の関係になる。

（1）毎分50Lの割合でプールに水を入れるとき、x分後のプールにたまった水yL
xとyの関係を式で表すと、y=50x
これは、一次関数なので○

（2）40円の鉛筆をx本と60円の消しゴムを買ったときの代金y円
xとyの関係を式で表すと、y=40x+60
これは、一次関数なので、○

（3）1辺の長さがxcmの正方形の面積ycm²
xとyの関係を式で表すと、y=x²
これは、一次関数でないので×

【対策問題】一次関数の変化の割合

（問1）1次関数y=2x+1について、次の表を完成して、xの値が1から3まで増加したときの、ｙの増加量/ｘの増加量を求めなさい。

＜表＞

ｘ	…	-3	-2	-1	0	1	2	3	…
ｙ	…	-5	-3	-1	1	3	5	7	…

（問2）一次関数y=6x-5で次の場合のyの増加量を求めなさい。
（1）xの増加量が3のとき
（2）xの増加量が-4のとき

（問3）次の問いに答えなさい。

1次関数ｙ＝3ｘ+6で、ｘの値が1から4まで増加したときの変化の割合を求めなさい。
1次関数ｙ＝-2ｘ+6で、ｘの値が1から4まで増加したときの変化の割合を求めなさい。
1次関数ｙ＝4ｘ+5で、ｘの増加量が5であるときの変化の割合を求めなさい。
1次関数ｙ＝4ｘ+6で、ｘの値が1から4まで増加したときのｘの増加量を求めなさい。
1次関数ｙ＝4ｘ-5で、ｘの値が－1から4まで増加したときのｘの増加量を求めなさい。
1次関数ｙ＝2ｘ+8で、ｘの値が1から4まで増加したときのｙの増加量を求めなさい。
1次関数ｙ＝-2ｘ+8で、ｘの値が1から3まで増加したときのｙの増加量を求めなさい。
1次関数ｙ＝3ｘ+2で、ｘの増加量が5であるときのｙの増加量を求めなさい。
1次関数ｙ＝aｘ+4で、ｘの増加量が5であるときのｙの増加量が10である。このとき、aの値を求めなさい。
1次関数ｙ＝aｘ-2で、ｘの値が-1から3まで増加したときのｙの増加量が8である。このとき、aの値を求めなさい。

【解答】

xの増加量に対するｙの増加量の割合を「変化の割合」といいます。1次関数y=ax+bでは変化の割合は一定で、aに等しくなります。

1次関数y=ax+bの変化の割合＝yの増加量/xの増加量

「きはじ」の要領で　ｙの増加量＝変化の割合（傾き）×ｘの増加量

（問1）
ｘ＝1のとき、ｙ＝2ｘ1+1＝3
ｘ＝3のとき、ｙ＝2×3+1＝7

したがって、xの増加量/ｙの増加量＝（7-3）/（3-1）＝2

（問2）
（1）18
（2）-24

（問3）

3
-2
4
3
5
6
-4
15
2
2

【対策問題】一次関数のグラフの特徴

次のＡ～Ｄの一次関数について、次の問いに記号で答えなさい。

グラフが右上がりの直線になるのは、直線Ａとどれか。
グラフが右下がりになる直線は、直線Ｂとどれか。
グラフがｙ軸の正の部分と交わるのは、直線Ｂとどれか。
グラフがｙ軸の負の部分と交わるのは、直線Ａとどれか。
ｘが増加すると、ｙは減少するのは、直線Ｂとどれか。
ｘが増加すると、ｙは増加するのは、直線Ａとどれか。
変化の割合が常に2である直線はどれか。
グラフがｙ軸の2と交わるのは、直線はどれか。
切片のｙ座標が一番小さい直線はどれか。
ｘの値2のとき、ｙの値が3となる直線はどれか。

【解答】

y=ax+bのグラフは、y=axのグラフをｙ軸の正の方向にbだけ平行に移動させた直線です。
a＞0のとき、ｘが増加すれば、ｙも増加する。
a＜0のとき、ｘが増加すれば、ｙを減少する。

【対策問題】一次関数の式を求める（傾きと切片がわかるとき）

次の問いに答えなさい。

傾きが2、切片が4である1次関数の式を求めよ。
変化の割合が4、切片が2である1次関数の式を求めよ。
直線ｙ＝3ｘと平行で、切片が2である1次関数の式を求めよ。
傾き2で、点（0,3）を通る直線の式を求めよ。
傾き-2で、ｘ＝0のとき、ｙ＝5を通る直線の式を求めよ。
変化の割合2で、点（0,3）を通る直線の式を求めよ。
直線ｙ＝3ｘ+5と平行で、点（0,2）を通る直線の式を求めよ。
直線ｙ＝5ｘ+5と平行で、点（0,-3）を通る直線の式を求めよ。
点（0,6）を通り、傾きが3である直線の式を求めよ。

【解答】

1次関数
2つの変数ｘ、ｙについて、ｙがｘの1次式で表されるとき、ｙはｘの1次関数であるといいます。1次関数は、一般的に「y=ax+b」とあらわされます。1年生で履修した比例式「y=ax」も1次関数であり、b=0の特別な式と理解できます。1次関数の式y=ax+b

a＝比例定数＝変化の割合＝ｙの増加量/ｘの増加量
b＝切片

ｙ＝2ｘ+4
ｙ＝4ｘ+2
ｙ＝3ｘ+2
ｙ＝2ｘ+3
ｙ＝-2ｘ+5
ｙ＝2ｘ+3
ｙ＝3ｘ+2
ｙ＝5ｘ-3
ｙ＝3ｘ+6

【対策問題】一次関数の式（傾きと1点の座標がわかるとき）

次の問いに答えなさい。

xが2増加すると、ｙが6増加し、切片が2である1次関数の式を求めよ。
2点（1,3）、（4,6）を通る直線の式を求めよ。
2点（1,1）、（3,-7）を通る直線の式を求めよ。
2点（3,5）、（4,8）を通る直線の式を求めよ。
2点（1,3）、（-2,9）を通る直線の式を求めよ。
傾きが2で点（2,1）を通る直線の式を求めよ。
傾きが-3で点（2,4）を通る直線の式を求めよ。
切片が2で点（2,10）を通る直線の式を求めよ。
切片が6で点（2,0）を通る直線の式を求めよ。
変化の割合が2で点（2,1）を通る直線の式を求めよ。
1次関数ｙ＝-3ｘ+6と平行で点（2,4）を通る直線の式を求めよ。

【解答】

1次関数y=ax+bにおいて、

aの値がわかるとき → 傾き、変化の割合、平行な直線がわかっている場合
bの値がわかるとき → 切片がわかっている場合

以上がわかっているときは、まずあてはめたのち、次に与えられている条件をあてはめていきます。またa,bの値がわからない2点が与えられている問題は、その2点をy=ax+bにそれぞれ代入して、連立方程式で解くか、先に、傾きをｘの増加量/ｙの増加量を利用して出して、解くかのいずれかです。

●例題
yがxの1次関数で、そのグラフが点（3,1）を通り、傾きが2であるとき、この1次関数を求めなさい。

＜解法＞

1次関数なので、y=ax+bとおく。
傾きが2なので、y=2x+bとおける。
（3,1）を通るので、代入。1＝2×3+b
これを解くと、b=-5
よって、y=-2x-5　となる。

ｙ＝3ｘ+2
ｙ＝ｘ+2
ｙ＝-4ｘ+5
ｙ＝3ｘ-4
ｙ＝-2ｘ+5
ｙ＝2ｘ-3
ｙ＝-3ｘ+10
ｙ＝4ｘ+2
ｙ＝-3ｘ+6
ｙ＝2ｘ-3
ｙ＝-3ｘ+10

【対策問題】一次関数の変域

次の問いに答えよ。

1次関数ｙ＝3ｘ+2で、ｘの変域が1≦ｘ≦3のとき、ｙの変域を求めよ。
1次関数ｙ＝ｘ+5で、ｘの変域が-1≦ｘ≦2のとき、ｙの変域を求めよ。
1次関数ｙ＝-2ｘ+4で、ｘの変域が2≦ｘ≦4のとき、ｙの変域を求めよ。
1次関数ｙ＝-4ｘ+2で、ｘの変域が-1≦ｘ≦2のとき、ｙの変域を求めよ。
1次関数ｙ＝2ｘ+1で、ｘの変域がｘ≦2のとき、ｙの変域を求めよ。
1次関数ｙ＝-3ｘ+5で、ｘの変域がｘ≦2のとき、ｙの変域を求めよ。
1次関数ｙ＝3ｘ+2で、ｘの変域が1＜ｘ≦3のとき、ｙの変域を求めよ。
1次関数ｙ＝ｘ+5で、ｘの変域が-1≦ｘ＜2のとき、ｙの変域を求めよ。
1次関数ｙ＝-2ｘ+4で、ｘの変域が2＜ｘ≦4のとき、ｙの変域を求めよ。
1次関数ｙ＝-4ｘ+2で、ｘの変域が-1≦ｘ＜2のとき、ｙの変域を求めよ。

【解答】

１次関数の変域

変数…いろいろな値をとることができる文字。ｘやｙを使います。これに対して、決まった値を示す数や文字を定数といいます。aやｂを使います。
変域…変数のとる値の範囲を変域といいます。一般的に、変域は、不等号を使って表します。

＜例＞

ことば…ｘは3以上、7より小さい（7未満）
不等号…3≦ｘ＜7

変域の例題
1次関数y=x-1について、ｘの変域が-2≦ｘ≦6のとき、ｙの変域を求めよ。

ｘ＝-2のとき、ｙ＝-2-1＝-3
ｘ＝6のとき、ｙ＝6-1＝5

よって、-3≦ｙ≦5となる。

一次関数の変域ポイント
それぞれ、代入して、小さい値を左、大きい値を右にし、不等号の向きに気をつけましょう。特に、傾きがマイナスのときに、注意が必要です。

5≦ｙ≦11
4≦ｙ≦7
-4≦ｙ≦0
-6≦ｙ≦6
ｙ≦5
ｙ≧-1
5＜ｙ≦11
4≦ｙ＜7
-4≦ｙ＜0
-6＜ｙ≦6

【対策問題】直線上にある座標を求める問題

次に問いに答えなさい。

2点（5,5）(2,5)の間の距離を求めよ。
2点（2,5）(2,8)の間の距離を求めよ。
2点（5,5）(-2,5)の間の距離を求めよ。
2点（2,5）(2,-8)の間の距離を求めよ。
2点（a+2,5）(a,5)の間の距離を求めよ。ただし、a＞0とする。
1次関数ｙ＝2ｘ+4において、ｘ＝1のときの、ｙの値を求めなさい。
1次関数ｙ＝－2ｘ+4において、ｙ＝2のときの、ｘの値を求めなさい。
点（ｔ、6）が、直線ｙ＝2ｘ+4上にあるとき、ｔの値を求めなさい。
点（8、ｔ）が、直線ｙ＝2ｘ+4上にあるとき、ｔの値を求めなさい。
点（4、10）が、直線ｙ＝2ｘ+ｔ上にあるとき、ｔの値を求めなさい。

【解答】

座標

座標軸…それぞれ原点で直角に交わる2つの数直線を考える。ｘ軸は、横の数直線。横軸ともいいます。ｙ軸は、縦の数直線。縦軸ともいいます。
原点O…座標軸の交点。
座標平面…座標軸の書かれている平面。

点の座標
点の位置を1組2つの数で表します。

点Pからｘ軸、ｙ軸に垂直な直線をひいたとき、ｘ軸と交わる点を目もりをPのｘ座標、ｙ軸と交わる点の目もりをPのｙ座標といいます。
Pのｘ座標がa、ｙ座標がbのとき、（a,b）と書き、Pの座標といいます。P(a,b)とも書きます。

点の位置の関係と座標
P(x,y)とする。

Pをｘ軸について折り返すと、(x,-y) →　ｘ軸に対称
Pをｙ軸について折り返すと、(-x,y) →　ｙ軸に対称
Pを原点Oについて180°回転すると、(-x,-y) → 原点Oに対称

1次関数の座標
与えられた値またはわかっている値をそれぞれ代入することで、求まることが多い。

【対策問題】連立方程式とグラフ（2直線の交点の求める問題）

次の問いに答えよ。

直線ｙ＝2ｘ+6とｙ軸との交点の座標を求めよ。
直線ｙ＝2ｘ+6とｘ軸との交点の座標を求めよ。
直線ｙ＝-2ｘ+4とｙ軸との交点の座標を求めよ。
直線ｙ＝-2ｘ+4とｘ軸との交点の座標を求めよ。
直線ｙ＝-1/2ｘ+4とｙ軸との交点の座標を求めよ。
直線ｙ＝-1/2ｘ+4 とｘ軸との交点の座標を求めよ。
2直線ｙ＝-ｘ+5とｙ＝2ｘ-1との交点の座標を求めよ。
2直線ｙ＝-ｘ+5とｙ＝ｘ-1との交点の座標を求めよ。
2直線ｙ＝-ｘ+13とｙ＝6ｘ+6との交点の座標を求めよ。
2直線ｙ＝-2ｘ+1とｙ＝-ｘ+3との交点の座標を求めよ。

【解答】

2直線の交点の求め方
2直線の交点の座標は、2つの直線の式を組にした連立方程式の解いて求められます。

（0,6）
（-3,0）
（0,4）
（2,0）
（0,4）
（8,0）
x＝2、y＝3
x＝3、y＝2
ｘ＝1、ｙ＝12
x＝-2、y＝5

【対策問題】一次関数の利用（道のり）

【問1】Aさんは、10時に家を出発して、自転車でｐ町まで行き、P町からは分速100ｍで歩いて家から11ｋｍはなれたQ町まで行きました。グラフは、Aさんが家を出発してからの時間をｘ分、家からの道のりをｙｋｍとしてｘとｙの関係を表したものです。これについて次の問いに答えなさい。

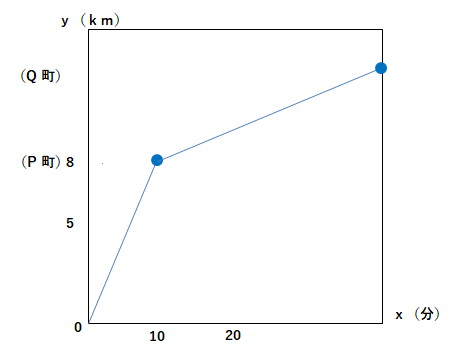
一次関数グラフ（自転車）

（1）自転車の速さは分速何ｍですか。
（2）家から出発して、Q町まで何分で到着しますか。
（3）家からQ地点までは、何ｋｍですか？

【問2】1ℓのガソリンで9ｋｍ走る自動車がある。この自動車に30ℓのガソリンを入れて出発した。ｘｋｍ走ったときの残りのガソリンをｙℓとするとき、次の問いに答えなさい。ただし、グラフは、このようすを表したものである。

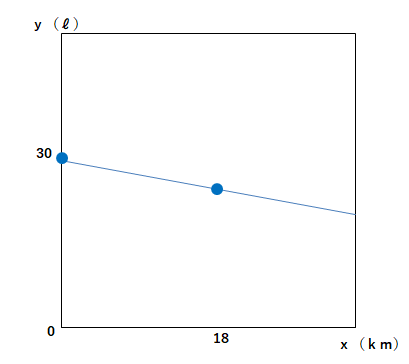
一次関数グラフ（ガソリン）

（1）1ｋｍ走るのにガソリンは何ℓ使うか、求めよ。
（2）ｙをｘの式で表せ。
（3）18ｋｍ走った時の残りのガソリンは何ℓか、求めよ。

【解答】
【問1】
（1）分速800ｍ
（2）40分
（3）11ｋｍ

【問2】
（1）1/9ℓ
（2）ｙ＝-1/9ｘ+30
（3）28ℓ

【対策問題】一次関数の利用（ろうそく）

長さ10ｃｍのろうそくに火をつけると、1分間に0.5ｃｍずつ短くなります。火をつけてからｘ分後のろうそくの長さをｙｃｍとすると次のようなグラフとなりました。問いに答えなさい。

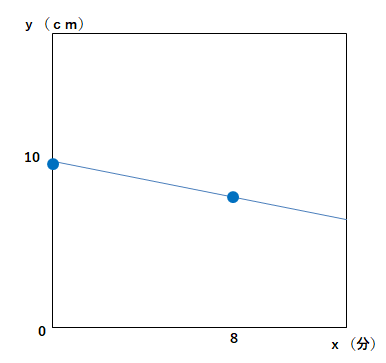
一次関数グラフ（ろうそく）

（1）5分後のろうそくの長さを求めよ。
（2）火をつけてからｘ分後のろうそくの長さをｙｃｍとして、ｙをｘの式を表しなさい。
（3）ろうそくが燃え尽きるのは何分後か求めよ。

【解答】
（1）7.5ｃｍ
（2）ｙ＝-0.5ｘ+10
（3）20分後

【対策問題】一次関数（水そう）

【問】40ℓ入る水そうがあります。今が水が5ℓ入っており、一定の割合で、水を入れていきます。水を入れ始めたから4分後に水そうの中の水の量は25ℓになりました。グラフは、これを表したものです。次の問いに答えなさい。

一次関数グラフ利用（水そう）

（1）1分間に水の量は、何ℓずつ増えますか？
（2）水を入れ始めてからx分後の水そうの中の水の量をｙℓとしてｙをｘの式を表しなさい。
（3）水そうが満杯になるのは、水を入れ始めたから何分後か。

【解答】
（1）5ℓ
（2）ｙ＝5ｘ+5
（3）7分後

【対策問題】一次関数（料金）

【問】Aさんは、スマートフォンの充電される電力の量とスマートフォンを使用した際の電力の消費される量について調べた。電池の残量は、百分率で表示され、充電は、6分に1％の割合で充電され、スマートフォンを使用するときは、1分に2％の割合で電力は消費されます。Aさんは、スマートフォンを充電しはじめ、24分後には、電池の残量は、54％であり、その後、充電をやめ、スマートフォンを電池の残量が0％になるまで使用を続けた。下のグラフは、Aさんが、スマートフォンを充電を始めてからｘ分後の電池の残量をｙ％とするとき、Aさんが、スマートフォンを使用を続けて電池の残量が0％になるまでのｘとｙの関係をグラフに表したものです。次の問いに答えなさい。