中3数学の「相似の証明」の解き方・仕方のまとめです。代表的なパターンの例題を見ながら、相似の証明についてみていきます。入試でも頻出度の高いところです。確実に習得しましょう。それでは、中3数学の「相似の証明」の解き方・仕方のまとめをみていきましょう。
いろいろな相似の証明の特訓練習問題
【問1】
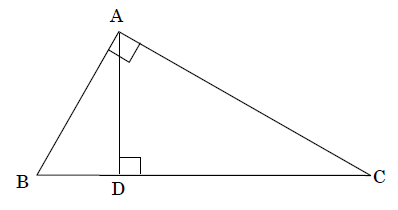
図には、∠A=90°である直角三角形ABCでAからBCに垂線ADをひきます。このとき、△ABCと△DBAであることを証明せよ。
【問2】

図には、∠A=90°である直角三角形ABCでAからBCに垂線ADをひきます。このとき、BC:BA=BA:BDであることを証明せよ。
【問3】
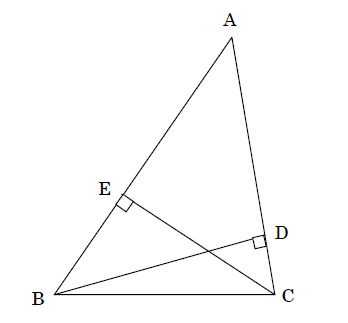
上の図の△ABCで、点B、Cから辺AC,ABにそれぞれ垂線BD,CEをひくとき、△ABD∽△ACEになることを証明しなさい。
いろいろな相似の証明の特訓練習問題の解答
【問1】
△ABCと△DBAにおいて
∠BAC=∠BDA=90°…①
∠Bは共通…②
①②より、2組の角がそれぞれ等しいので、
△ABC∽△DBA
【問2】
△ABCと△DBAにおいて
∠BAC=∠BDA=90°…①
∠Bは共通…②
①②より、2組の角がそれぞれ等しいので、
△ABC∽△DBA
相似な図形の対応をする辺の比は等しいから
BC:BA=BA:BD
∠BAC=∠BDA=90°…①
∠ACB=∠DAB…②
①②より2組の角がそれぞれ等しいので、
△ABC∽△DBA
ここで、∠ACB=∠DABは、条件にないので、使用することはできません。条件にないものは、使えない!これは覚えておきましょう。
【問3】
△ABDと△ACEにおいて
∠BDA=CEA=90°…①
∠Aは共通…②
①②より2組の角がそれぞれ等しいので、
△ABD∽△ACE
以上が、中3数学の「相似の証明」の解き方・仕方のまとめです。三角形の相似条件は、「3組の辺の比がすべて等しい。」「2組の辺の比とその間の角がそれぞれ等しい。」「2組の角がそれぞれ等しい。」なので、まずは、「2組の角がそれぞれ等しい。」が使えないかということから、証明問題は解き始めます。今回は、いずれも、「2組の角がそれぞれ等しい。」だったように、非常に、「2組の角がそれぞれ等しい。」という条件になることが多いです。

コメント