中学3年生の数学で学ぶ「三平方の定理」は、直角三角形の辺の関係を利用して長さを求める基本公式です。中でも「点から直線に垂線を下ろす長さを求める」問題は、図形の理解力と三平方の定理の活用力が問われる応用問題として、定期テストや高校入試でもよく出題されます。この記事では、垂線の長さの求め方や問題パターン、計算時の注意点を図を用いながら丁寧に解説します。苦手意識を克服し、得点アップを目指しましょう!
垂線を下ろした長さを求める問題(中3数三平方の定理)
【問1】次の立方体について、以下の各問いに答えなさい。
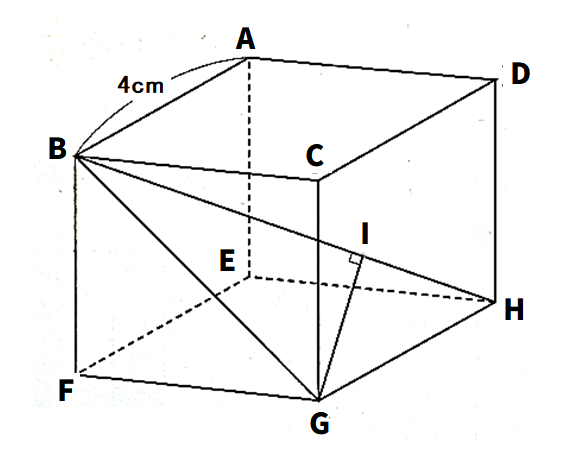
(1) △BGHの面積を求めなさい。
(2) BHの長さを求めなさい。
(3) 頂点Gから辺BHに垂線を下ろし交点をIとするときのGIの長さを求めなさい。
【問2】次の立方体について、以下の各問いに答えなさい。
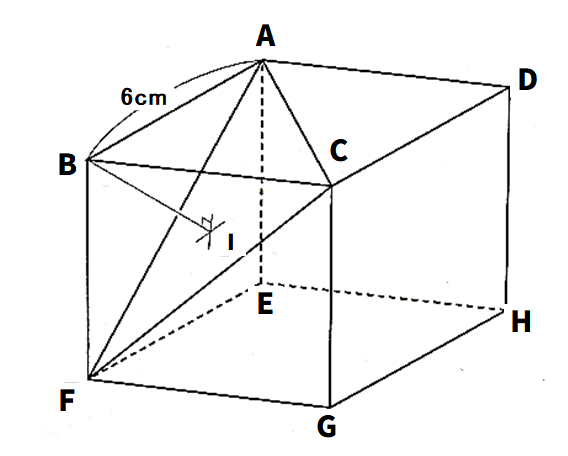
(1) 三角すいB-AFCの体積を求めなさい。
(2)△AFCの面積を求めなさい。
(3) 頂点BからAFCに垂線を下ろし交点をIとするときのBIの長さを求めなさい。
垂線を下ろした長さを求める問題(中3数三平方の定理)の解答
【問1】
(1)8√2cm2
(2)4√3cm
(3)4√6/3cm
【問2】
(1)36cm3
(2)18√2cm2
(3)2√3cm



コメント