中2数学「後期期末テスト定期テスト過去問分析問題」です。後期期末テストが近づいてきましたね。今回のテスト範囲は「合同な図形」と「図形の角度」が中心。三角形の合同条件や証明問題、平行線と角の関係など、しっかり理解しておくべき重要な単元です。
「証明問題の書き方がわからない…」「どの合同条件を使えばいいのか迷う…」「角度の関係が複雑で混乱する…」と感じている人もいるかもしれません。でも、基本の考え方を押さえて練習すれば、確実に得点できる単元です!この記事では、テストによく出る問題を厳選し、解き方のポイントをわかりやすく解説します。しっかり復習して、自信を持ってテストに挑みましょう!
| テスト | 範囲 |
|---|---|
| 中1数学 前期中間 | 正負の数・指数計算・四則計算 |
| 中1数学 前期期末 | 一次方程式 |
| 中1数学 後期中間 | 比例反比例 |
| 中1数学 後期期末 | 平面・空間図形・資料の整理 |
| 中2数学 前期中間 | 文字式の計算 |
| 中2数学 前期期末 | 連立方程式 |
| 中2数学 後期中間 | 一次関数 |
| 【今回】中2数学 後期期末 | 図形の性質と証明・確率 |
| 中3数学 前期中間 | 展開・因数分解・平方根 |
| 中3数学 前期期末 | 二次方程式 |
| 中3数学 後期中間 | 二次関数 |
| 中3数学 後期期末 | 相似・三平方の定理 |
| ※テスト範囲が違うときは、上記を参照にリンク先へ | |
(中2数)後期期末テスト定期テスト過去問分析問題
問1 次の( )にあてはまることばや数を書きなさい。
(1)用語や記号などの意味をはっきり述べるものを( ① )という。証明されたことがらのうちで、よく使われるものを( ② )という。
(2)2直線が交わるときにできる4つの角のうち、( ③ )は等しい。平行な2直線に1直線に交わるとき、( ④ )や( ⑤ )は等しい。
(3)三角形の内角の和は( ⑥ )°である。三角形の( ⑦ )はそれととなりあわない内角の和に等しい。
(4)二等辺三角形の2つの( ⑧ )は等しい。二等辺三角形の( ⑨ )の二等分線は( ⑩ )を垂直に2等分する。
(5)直角三角形で、直角に対する辺を( ⑪ )という。
問2 次のことがらの逆を書き、それが正しいもには〇、正しくないものには×をつけなさい。
(1)4の倍数ならば、2の倍数である。
(2)△ABCと△DEFで、△ABC=△EDFならば、∠B=∠Eである。
(3)△ABCで、AB=ACならば、∠B=∠Cである。
問3 次のような四角形ABCDは、平行四辺形であるといってよか、平行四辺形になるものは〇、ならないものは×をつけなさい。
(1)AB=8cm、BC=5cm、CD=5cm、DA=8cm
(2)∠A=80°、∠B=100°、AD=5cm、BC=5cm
(3)対角線の交点をOとすると、OA=6cm、OB=6cm、OC=5cm、OD=5cm
(4)∠A=∠B=70°、∠C=∠D=110°
問4 次の中から合同な三角形を選び、記号≡を使って表しなさい。また、それぞれの合同条件を書きなさい。
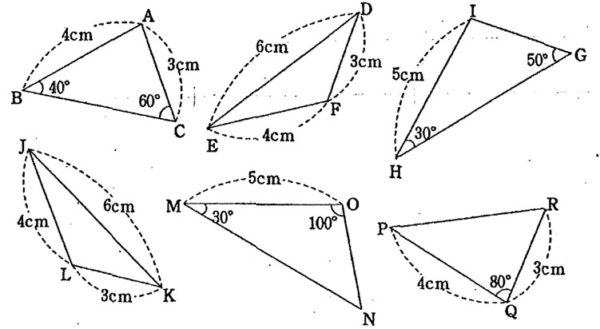
問5 次の図で、合同な三角形の組を、記号≡を使って表しなさい。また、それぞれの合同条件を書きなさい。
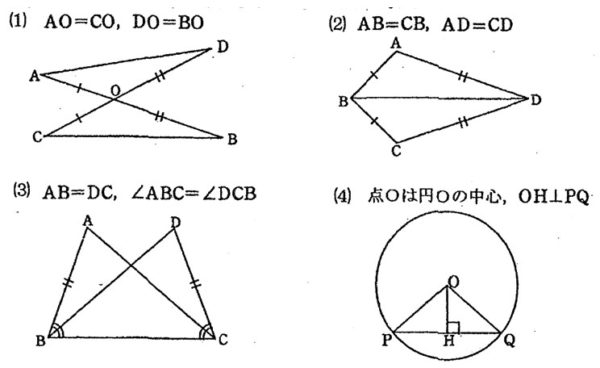
問6 下の図で、四角形ABCDは平行四辺形です。次の問いに答えなさい。
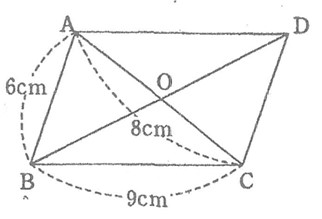
(1)辺AD、辺CD、線分COの長さを求めなさい。
(2)∠ABC、∠ACDと等しい角をそれぞれ求めなさい。
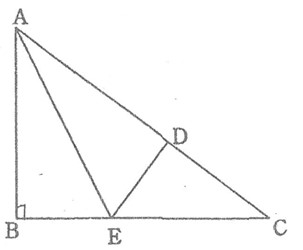
問7 次の図で、∠xの大きさを求めなさい。
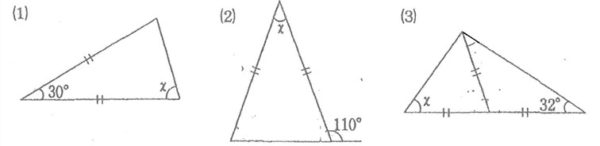
問8 次の図の平行四辺形ABCDで、∠xの大きさを求めなさい。
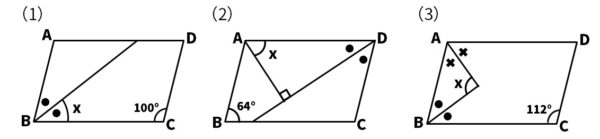
問9 次の図で、△ABCは∠B=90°の直角三角形です。点Dは辺ACの点で、AB=ADです。点Dを通る辺ACの垂線と辺BCの交点をEとし、点Aと点Eを結びます。このとき、BE=DEであることを証明しなさい。
(中2数)後期期末テスト定期テスト過去問分析問題の解答
問1
①定義
②定理
③対頂角
④同位角
⑤錯角
⑥180
⑦外角
⑧底角
⑨頂角
⑩底辺
⑪斜辺
問2
(1)2の倍数ならば、4の倍数である。(×)
(2)△ABCと△DEFで、∠B=∠Eならば、△ABC≡△EDFである。(×)
(3)△ABCで、∠B=∠Cならば、AB=ACである。(○)
問3
(1)×
(2)○
(3)×
(4)○
問4
(1)△ABL≡△QPR 2辺とその間の角がそれぞれ等しい
(2)△DEF≡△KJL 3辺がそれぞれ等しい
(3)△GHI≡△NMO 1辺とその両端の角がそれぞれ等しい
問5
(1)△AOD≡△COB 2辺とその間の角がそれぞれ等しい
(2)△ABD≡△CBD 3辺がそれぞれ等しい
(3)△ABC≡△DCB 2辺とその間の角がそれぞれ等しい
(4)△OHP≡△OHQ 直角三角形の斜辺と他の1辺がそれぞれ等しい
問6
(1)AD=9cm CD=6cm CO=4cm
(2)∠ABC=∠CDA ∠ACD=∠CAB
問7
(1)∠x=75°
(2)∠x=40°
(3)∠x=58°
問8
(1)∠x=40°
(2)∠x=58°
(3)∠x=90°
問9
△ABEと△ADEにおいて
仮定より AB=AD…①
共通な辺だから AE=AE…②
辺ACの垂線と辺BCの交点をEとしているから
∠ABE=∠ADE=90°…③
①②③より直角三角形の斜辺と他の1辺がそれぞれ等しいので、
△ABE≡△ADE
対応する辺の長さは等しいから
BE=DE


コメント